Advertisements
Advertisements
Question
The difference between any two consecutive interior angles of a polygon is 5°. If the smallest angle is 120°, find the number of the sides of the polygon.
Solution
The angles of the polygon will form an A.P. with common difference d as 5° and first term a as 120°.
It is known that the sum of all angles of a polygon with n sides is 180° (n – 2).
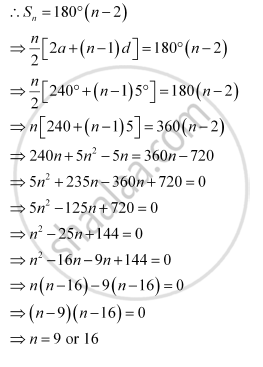
APPEARS IN
RELATED QUESTIONS
Find the sum of all natural numbers lying between 100 and 1000, which are multiples of 5.
In an A.P, the first term is 2 and the sum of the first five terms is one-fourth of the next five terms. Show that 20th term is –112.
If the sum of a certain number of terms of the A.P. 25, 22, 19, … is 116. Find the last term
The sums of n terms of two arithmetic progressions are in the ratio 5n + 4: 9n + 6. Find the ratio of their 18th terms
If the sum of first p terms of an A.P. is equal to the sum of the first q terms, then find the sum of the first (p + q) terms.
Find the sum of all two digit numbers which when divided by 4, yields 1 as remainder.
Shamshad Ali buys a scooter for Rs 22000. He pays Rs 4000 cash and agrees to pay the balance in annual installment of Rs 1000 plus 10% interest on the unpaid amount. How much will the scooter cost him?
A man deposited Rs 10000 in a bank at the rate of 5% simple interest annually. Find the amount in 15th year since he deposited the amount and also calculate the total amount after 20 years.
Let < an > be a sequence. Write the first five term in the following:
a1 = 1 = a2, an = an − 1 + an − 2, n > 2
The nth term of a sequence is given by an = 2n + 7. Show that it is an A.P. Also, find its 7th term.
Which term of the A.P. 84, 80, 76, ... is 0?
Find the sum of the following serie:
2 + 5 + 8 + ... + 182
Find the sum of all even integers between 101 and 999.
Solve:
25 + 22 + 19 + 16 + ... + x = 115
Find the r th term of an A.P., the sum of whose first n terms is 3n2 + 2n.
The first term of an A.P. is 2 and the last term is 50. The sum of all these terms is 442. Find the common difference.
If Sn = n2 p and Sm = m2 p, m ≠ n, in an A.P., prove that Sp = p3.
If 12th term of an A.P. is −13 and the sum of the first four terms is 24, what is the sum of first 10 terms?
If the sum of n terms of an A.P. is nP + \[\frac{1}{2}\] n (n − 1) Q, where P and Q are constants, find the common difference.
If \[\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\] are in A.P., prove that:
\[\frac{b + c}{a}, \frac{c + a}{b}, \frac{a + b}{c}\] are in A.P.
If a2, b2, c2 are in A.P., prove that \[\frac{a}{b + c}, \frac{b}{c + a}, \frac{c}{a + b}\] are in A.P.
A man arranges to pay off a debt of Rs 3600 by 40 annual instalments which form an arithmetic series. When 30 of the instalments are paid, he dies leaving one-third of the debt unpaid, find the value of the first instalment.
A piece of equipment cost a certain factory Rs 600,000. If it depreciates in value, 15% the first, 13.5% the next year, 12% the third year, and so on. What will be its value at the end of 10 years, all percentages applying to the original cost?
A man starts repaying a loan as first instalment of Rs 100 = 00. If he increases the instalments by Rs 5 every month, what amount he will pay in the 30th instalment?
Write the value of n for which n th terms of the A.P.s 3, 10, 17, ... and 63, 65, 67, .... are equal.
If m th term of an A.P. is n and nth term is m, then write its pth term.
If the sum of p terms of an A.P. is q and the sum of q terms is p, then the sum of p + q terms will be
If the sum of n terms of an A.P. be 3 n2 − n and its common difference is 6, then its first term is
If the sum of n terms of an A.P. is 2 n2 + 5 n, then its nth term is
If four numbers in A.P. are such that their sum is 50 and the greatest number is 4 times the least, then the numbers are
If second, third and sixth terms of an A.P. are consecutive terms of a G.P., write the common ratio of the G.P.
If for an arithmetic progression, 9 times nineth term is equal to 13 times thirteenth term, then value of twenty second term is ____________.
The first term of an A.P. is a, the second term is b and the last term is c. Show that the sum of the A.P. is `((b + c - 2a)(c + a))/(2(b - a))`.
If the sum of p terms of an A.P. is q and the sum of q terms is p, show that the sum of p + q terms is – (p + q). Also, find the sum of first p – q terms (p > q).
If in an A.P., Sn = qn2 and Sm = qm2, where Sr denotes the sum of r terms of the A.P., then Sq equals ______.
Any term of an A.P. (except first) is equal to half the sum of terms which are equidistant from it.
The sum of n terms of an AP is 3n2 + 5n. The number of term which equals 164 is ______.
