Advertisements
Advertisements
प्रश्न
The difference between any two consecutive interior angles of a polygon is 5°. If the smallest angle is 120°, find the number of the sides of the polygon.
उत्तर
The angles of the polygon will form an A.P. with common difference d as 5° and first term a as 120°.
It is known that the sum of all angles of a polygon with n sides is 180° (n – 2).
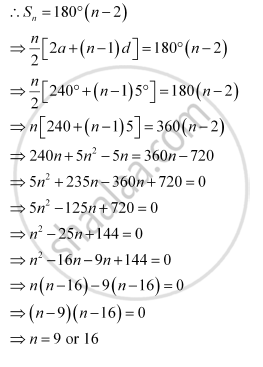
APPEARS IN
संबंधित प्रश्न
Find the sum of odd integers from 1 to 2001.
If the sum of first p terms of an A.P. is equal to the sum of the first q terms, then find the sum of the first (p + q) terms.
Show that the sum of (m + n)th and (m – n)th terms of an A.P. is equal to twice the mth term.
Find the sum of all numbers between 200 and 400 which are divisible by 7.
Show that the following sequence is an A.P. Also find the common difference and write 3 more terms in case.
−1, 1/4, 3/2, 11/4, ...
Find:
10th term of the A.P. 1, 4, 7, 10, ...
Find:
18th term of the A.P.
\[\sqrt{2}, 3\sqrt{2}, 5\sqrt{2},\]
Find:
nth term of the A.P. 13, 8, 3, −2, ...
Which term of the sequence 12 + 8i, 11 + 6i, 10 + 4i, ... is purely real ?
If the nth term of the A.P. 9, 7, 5, ... is same as the nth term of the A.P. 15, 12, 9, ... find n.
Find the 12th term from the following arithmetic progression:
3, 5, 7, 9, ... 201
The angles of a quadrilateral are in A.P. whose common difference is 10°. Find the angles.
Find the sum of the following arithmetic progression :
50, 46, 42, ... to 10 terms
Find the sum of the following arithmetic progression :
3, 9/2, 6, 15/2, ... to 25 terms
Find the sum of the following arithmetic progression :
\[\frac{x - y}{x + y}, \frac{3x - 2y}{x + y}, \frac{5x - 3y}{x + y}\], ... to n terms.
Find the sum of the following serie:
2 + 5 + 8 + ... + 182
Find the sum of all even integers between 101 and 999.
Find the sum of all those integers between 100 and 800 each of which on division by 16 leaves the remainder 7.
The sum of first 7 terms of an A.P. is 10 and that of next 7 terms is 17. Find the progression.
If a, b, c is in A.P., then show that:
bc − a2, ca − b2, ab − c2 are in A.P.
A man saved Rs 16500 in ten years. In each year after the first he saved Rs 100 more than he did in the receding year. How much did he save in the first year?
A manufacturer of radio sets produced 600 units in the third year and 700 units in the seventh year. Assuming that the product increases uniformly by a fixed number every year, find (i) the production in the first year (ii) the total product in 7 years and (iii) the product in the 10th year.
A piece of equipment cost a certain factory Rs 600,000. If it depreciates in value, 15% the first, 13.5% the next year, 12% the third year, and so on. What will be its value at the end of 10 years, all percentages applying to the original cost?
A carpenter was hired to build 192 window frames. The first day he made five frames and each day thereafter he made two more frames than he made the day before. How many days did it take him to finish the job?
In a cricket team tournament 16 teams participated. A sum of ₹8000 is to be awarded among themselves as prize money. If the last place team is awarded ₹275 in prize money and the award increases by the same amount for successive finishing places, then how much amount will the first place team receive?
Write the sum of first n odd natural numbers.
If four numbers in A.P. are such that their sum is 50 and the greatest number is 4 times the least, then the numbers are
If n arithmetic means are inserted between 1 and 31 such that the ratio of the first mean and nth mean is 3 : 29, then the value of n is
Let Sn denote the sum of n terms of an A.P. whose first term is a. If the common difference d is given by d = Sn − k Sn − 1 + Sn − 2 , then k =
If, S1 is the sum of an arithmetic progression of 'n' odd number of terms and S2 the sum of the terms of the series in odd places, then \[\frac{S_1}{S_2}\] =
If in an A.P., Sn = n2p and Sm = m2p, where Sr denotes the sum of r terms of the A.P., then Sp is equal to
If second, third and sixth terms of an A.P. are consecutive terms of a G.P., write the common ratio of the G.P.
The first three of four given numbers are in G.P. and their last three are in A.P. with common difference 6. If first and fourth numbers are equal, then the first number is
If the sum of m terms of an A.P. is equal to the sum of either the next n terms or the next p terms, then prove that `(m + n) (1/m - 1/p) = (m + p) (1/m - 1/n)`
If the sum of n terms of an A.P. is given by Sn = 3n + 2n2, then the common difference of the A.P. is ______.
If n AM's are inserted between 1 and 31 and ratio of 7th and (n – 1)th A.M. is 5:9, then n equals ______.
If the first term of an A.P. is 3 and the sum of its first 25 terms is equal to the sum of its next 15 terms, then the common difference of this A.P. is ______.
If b2, a2, c2 are in A.P., then `1/(a + b), 1/(b + c), 1/(c + a)` will be in ______
