Advertisements
Advertisements
प्रश्न
`cot[cos^-1 (7/25)]` का मान है।
विकल्प
`25/24`
`25/7`
`24/25`
`7/24`
उत्तर
सही उत्तर `underline(7/24)`है।
व्याख्या:
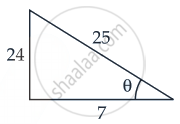
हमारे पास, `cot[cos^-1 (7/25)]`
माना `cos^-1 7/25` = θ
∴ cos θ = `7/25`
⇒ cot θ = `7/24`
∴ `cot[cos^-1 (7/25)] = cot[cot^-1 (7/24)] = 7/24`
APPEARS IN
संबंधित प्रश्न
`tan^-1 sqrt(3) - sec^-1(-2)` का मान ज्ञात कीजिए।
`sin^-1 [cos(sin^-1 sqrt(3)/2)]` का मान ज्ञात कीजिए।
`sec(tan^-1 y/2)` का मान ज्ञात कीजिए।
`tan^-1((1 - x)/(1 + x)) = 1/2 tan^-1x, x > 0` को x के लिए हल कीजिए।
x के वे मान ज्ञात कीजिए जो समीकरण sin–1x + sin–1(1 – x) = cos–1x को संतुष्ट करते हैं।
समीकरण `sin^-1 6x + sin^-1 6sqrt(3)x = - pi/2` को हल कीजिए।
मुख्य मान शाखा के अतिरिक्त cos-1 की एक अन्य शाखा है।
व्यंजक cos–1[cos (– 680°)] का मान है।
यदि θ = sin–1 (sin (– 600°), तब θ का मान है।
फलन y = sin–1 (- x2) का प्रांत है।
f(x) = sin–1x + cosx द्वारा परिभाषित फलन का प्रांत है।
`tan(cos^-1 3/5 + tan^-1 1/4)` का मान है।
यदि α ≤ 2 sin–1x + cos–1x ≤ β, तब
`cos[cos^-1 ((-sqrt(3))/2) + pi/6]` का मान ज्ञात कीजिए।
सिद्ध कीजिए कि `cot(pi/4 - 2cot^-1 3)` = 7
व्यंजक `sin(2tan^-1 1/3) + cos(tan^-1 2sqrt(2))` का मान निकालिए।
यदि 2 tan-1(cos ) = tan-1(2 cosec ), तो दिखाइए कि θ = `π /4`.
दर्शाइए कि `cos(2tan^-1 1/7) = sin(4tan^-1 1/3)`
सिद्ध कीजिए कि `sin^-1 8/17 + sin^-1 3/5 = sin^-1 77/85`
निम्न में से कौन सा cos-1x की मुख्य शाखा है?
यदि 3 tan-1x + cot-1x = , तो x बराबर होता है।
यदि `cos(sin^-1 2/5 + cos^-1x)` = 0 , तो x का मान है।
व्यंजक `2 sec^-1 2 + sin^-1 (1/2)` का मान है।
यदि tan–1x + tan–1y = `(4pi)/5`, तो cot–1x + cot–1y बराबर है।
`cos^-1 (- 1/2)` की मूख्य शाखा ______ है।
`tan^-1 sqrt(3)` का मुख्य मान ______ है।
`cos^-1 (cos (14pi)/3)` का मान ______ है।
व्यंजक `tan((sin^-1x + cos^-1x)/2)`, जहाँ x = `sqrt(3)/2` है, का मान ______ है।
प्रत्येक त्रिकोणमितीय फलन का उनके संगत प्रांतों में प्रतिलोम फलन का अस्तित्व होता है।
