Advertisements
Advertisements
प्रश्न
Find the sum of integers from 1 to 100 that are divisible by 2 or 5.
उत्तर
The integers from 1 to 100, which are divisible by 2, are 2, 4, 6… 100.
This forms an A.P. with both the first term and common difference equal to 2.
⇒100 = 2 + (n –1) 2
⇒ n = 50

The integers from 1 to 100, which are divisible by 5, are 5, 10… 100.
This forms an A.P. with both the first term and common difference equal to 5.
∴100 = 5 + (n –1) 5
⇒ 5n = 100
⇒ n = 20
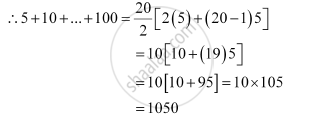
The integers, which are divisible by both 2 and 5, are 10, 20, … 100.
This also forms an A.P. with both the first term and common difference equal to 10.
∴100 = 10 + (n –1) (10)
⇒ 100 = 10n
⇒ n = 10
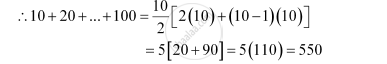
∴Required sum = 2550 + 1050 – 550 = 3050
Thus, the sum of the integers from 1 to 100, which are divisible by 2 or 5, is 3050.
APPEARS IN
संबंधित प्रश्न
How many terms of the A.P. -6 , `-11/2` , -5... are needed to give the sum –25?
Find the sum to n terms of the A.P., whose kth term is 5k + 1.
Find the sum of all two digit numbers which when divided by 4, yields 1 as remainder.
Show that the following sequence is an A.P. Also find the common difference and write 3 more terms in case.
3, −1, −5, −9 ...
Find the sum of the following arithmetic progression :
a + b, a − b, a − 3b, ... to 22 terms
Find the sum of all integers between 50 and 500 which are divisible by 7.
The third term of an A.P. is 7 and the seventh term exceeds three times the third term by 2. Find the first term, the common difference and the sum of first 20 terms.
The first term of an A.P. is 2 and the last term is 50. The sum of all these terms is 442. Find the common difference.
The number of terms of an A.P. is even; the sum of odd terms is 24, of the even terms is 30, and the last term exceeds the first by \[10 \frac{1}{2}\] ,find the number of terms and the series.
If 12th term of an A.P. is −13 and the sum of the first four terms is 24, what is the sum of first 10 terms?
Find the sum of n terms of the A.P. whose kth terms is 5k + 1.
Find the sum of odd integers from 1 to 2001.
If S1 be the sum of (2n + 1) terms of an A.P. and S2 be the sum of its odd terms, then prove that: S1 : S2 = (2n + 1) : (n + 1).
Find an A.P. in which the sum of any number of terms is always three times the squared number of these terms.
The sums of first n terms of two A.P.'s are in the ratio (7n + 2) : (n + 4). Find the ratio of their 5th terms.
If \[\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\] are in A.P., prove that:
a (b +c), b (c + a), c (a +b) are in A.P.
Insert five numbers between 8 and 26 such that the resulting sequence is an A.P.
The income of a person is Rs 300,000 in the first year and he receives an increase of Rs 10000 to his income per year for the next 19 years. Find the total amount, he received in 20 years.
Write the sum of first n even natural numbers.
Write the value of n for which n th terms of the A.P.s 3, 10, 17, ... and 63, 65, 67, .... are equal.
If the sums of n terms of two AP.'s are in the ratio (3n + 2) : (2n + 3), then find the ratio of their 12th terms.
If 7th and 13th terms of an A.P. be 34 and 64 respectively, then its 18th term is
If the sum of p terms of an A.P. is q and the sum of q terms is p, then the sum of p + q terms will be
If the sum of n terms of an A.P. be 3 n2 − n and its common difference is 6, then its first term is
If the sum of n terms of an A.P. is 2 n2 + 5 n, then its nth term is
If a1, a2, a3, .... an are in A.P. with common difference d, then the sum of the series sin d [sec a1 sec a2 + sec a2 sec a3 + .... + sec an − 1 sec an], is
If four numbers in A.P. are such that their sum is 50 and the greatest number is 4 times the least, then the numbers are
If n arithmetic means are inserted between 1 and 31 such that the ratio of the first mean and nth mean is 3 : 29, then the value of n is
If the sum of first n even natural numbers is equal to k times the sum of first n odd natural numbers, then k =
Mark the correct alternative in the following question:
If in an A.P., the pth term is q and (p + q)th term is zero, then the qth term is
If second, third and sixth terms of an A.P. are consecutive terms of a G.P., write the common ratio of the G.P.
Write the quadratic equation the arithmetic and geometric means of whose roots are Aand G respectively.
Show that (x2 + xy + y2), (z2 + xz + x2) and (y2 + yz + z2) are consecutive terms of an A.P., if x, y and z are in A.P.
If a1, a2, ..., an are in A.P. with common difference d (where d ≠ 0); then the sum of the series sin d (cosec a1 cosec a2 + cosec a2 cosec a3 + ...+ cosec an–1 cosec an) is equal to cot a1 – cot an
If a, b, c, d are four distinct positive quantities in A.P., then show that bc > ad
A man saved Rs 66000 in 20 years. In each succeeding year after the first year he saved Rs 200 more than what he saved in the previous year. How much did he save in the first year?
Let Sn denote the sum of the first n terms of an A.P. If S2n = 3Sn then S3n: Sn is equal to ______.
