Advertisements
Advertisements
प्रश्न
if `tan theta = 3/4`, find the value of `(1 - cos theta)/(1 +cos theta)`
उत्तर
Given tan = 3/4
We have to find the value of the expression `(1 - cos theta)/(1 + cos theta)`
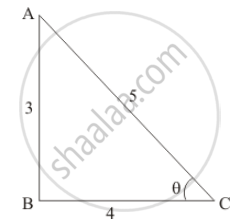
From the above figure, we have
`AC = sqrt(AB^2 + BC^2)`
`= sqrt(3^2 + 4^2)`
= 5
`cos theta = 4/5`
Therefore
`(1 - cos theta)/(1 + cos theta) = (1 - 4/5)/(1 +4/5)`
`= 1/9`
Hence, the value of the given expression is 1/9
APPEARS IN
संबंधित प्रश्न
If the angle θ = -60° , find the value of sinθ .
if `sqrt3 tan theta = 3 sin theta` find the value of `sin^2 theta - cos^2 theta`
Evaluate.
`cos^2 26^@+cos65^@sin26^@+tan36^@/cot54^@`
Express the following in terms of angles between 0° and 45°:
cos74° + sec67°
Evaluate:
tan(55° - A) - cot(35° + A)
Find the value of x, if sin x = sin 60° cos 30° – cos 60° sin 30°
Use tables to find sine of 10° 20' + 20° 45'
Use tables to find cosine of 8° 12’
Use tables to find the acute angle θ, if the value of sin θ is 0.4848
Prove that:
`1/(1 + sin(90^@ - A)) + 1/(1 - sin(90^@ - A)) = 2sec^2(90^@ - A)`
∠ACD is an exterior angle of Δ ABC. If ∠B = 40o, ∠A = 70o find ∠ACD.
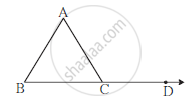
Given
\[\frac{4 \cos \theta - \sin \theta}{2 \cos \theta + \sin \theta}\] what is the value of \[\frac{{cosec}^2 \theta - \sec^2 \theta}{{cosec}^2 \theta + \sec^2 \theta}\]
If 5 tan θ − 4 = 0, then the value of \[\frac{5 \sin \theta - 4 \cos \theta}{5 \sin \theta + 4 \cos \theta}\] is:
If 8 tan x = 15, then sin x − cos x is equal to
If θ and 2θ − 45° are acute angles such that sin θ = cos (2θ − 45°), then tan θ is equal to
If A, B and C are interior angles of a triangle ABC, then \[\sin \left( \frac{B + C}{2} \right) =\]
In the following figure the value of cos ϕ is

Evaluate: `3(sin72°)/(cos18°) - (sec32°)/("cosec"58°)`.
Find the value of the following:
`cot theta/(tan(90^circ - theta)) + (cos(90^circ - theta) tantheta sec(90^circ - theta))/(sin(90^circ - theta)cot(90^circ - theta)"cosec"(90^circ - theta))`
In ∆ABC, cos C = `12/13` and BC = 24, then AC = ?
