Advertisements
Advertisements
Question
if `tan theta = 3/4`, find the value of `(1 - cos theta)/(1 +cos theta)`
Solution
Given tan = 3/4
We have to find the value of the expression `(1 - cos theta)/(1 + cos theta)`
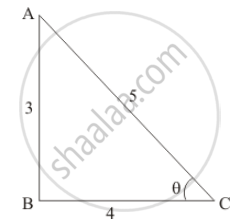
From the above figure, we have
`AC = sqrt(AB^2 + BC^2)`
`= sqrt(3^2 + 4^2)`
= 5
`cos theta = 4/5`
Therefore
`(1 - cos theta)/(1 + cos theta) = (1 - 4/5)/(1 +4/5)`
`= 1/9`
Hence, the value of the given expression is 1/9
APPEARS IN
RELATED QUESTIONS
Evaluate `(sin 18^@)/(cos 72^@)`
Show that cos 38° cos 52° − sin 38° sin 52° = 0
What is the value of (cos2 67° – sin2 23°)?
Evaluate.
sin(90° - A) cosA + cos(90° - A) sinA
Express the following in terms of angle between 0° and 45°:
sin 59° + tan 63°
Evaluate:
3cos80° cosec10° + 2 sin59° sec31°
Evaluate:
cosec (65° + A) – sec (25° – A)
Evaluate:
`2 tan57^circ/(cot33^circ) - cot70^circ/(tan20^circ) - sqrt(2) cos45^circ`
Evaluate:
`(cot^2 41^circ)/(tan^2 49^circ) - 2 sin^2 75^circ/cos^2 15^circ`
Evaluate:
3 cos 80° cosec 10° + 2 cos 59° cosec 31°
If A + B = 90° and \[\tan A = \frac{3}{4}\]\[\tan A = \frac{3}{4}\] what is cot B?
If 5 tan θ − 4 = 0, then the value of \[\frac{5 \sin \theta - 4 \cos \theta}{5 \sin \theta + 4 \cos \theta}\] is:
If 16 cot x = 12, then \[\frac{\sin x - \cos x}{\sin x + \cos x}\]
In the following figure the value of cos ϕ is

If ∆ABC is right angled at C, then the value of cos (A + B) is ______.
Prove the following.
tan4θ + tan2θ = sec4θ - sec2θ
Evaluate: cos2 25° - sin2 65° - tan2 45°
In the given figure, if AB = 14 cm, BD = 10 cm and DC = 8 cm, then the value of tan B is ______.

2(sin6 θ + cos6 θ) – 3(sin4 θ + cos4 θ) is equal to ______.
The value of (tan1° tan2° tan3° ... tan89°) is ______.
