Advertisements
Advertisements
प्रश्न
if `tan theta = 3/4`, find the value of `(1 - cos theta)/(1 +cos theta)`
उत्तर
Given tan = 3/4
We have to find the value of the expression `(1 - cos theta)/(1 + cos theta)`
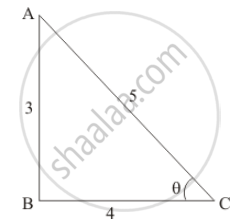
From the above figure, we have
`AC = sqrt(AB^2 + BC^2)`
`= sqrt(3^2 + 4^2)`
= 5
`cos theta = 4/5`
Therefore
`(1 - cos theta)/(1 + cos theta) = (1 - 4/5)/(1 +4/5)`
`= 1/9`
Hence, the value of the given expression is 1/9
APPEARS IN
संबंधित प्रश्न
If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A
Solve.
`sec75/(cosec15)`
Solve.
sin15° cos75° + cos15° sin75°
Solve.
sin42° sin48° - cos42° cos48°
Evaluate.
sin235° + sin255°
Evaluate.
`cot54^@/(tan36^@)+tan20^@/(cot70^@)-2`
Express the following in terms of angle between 0° and 45°:
sin 59° + tan 63°
Express the following in terms of angles between 0° and 45°:
cosec68° + cot72°
For triangle ABC, show that : `sin (A + B)/2 = cos C/2`
Evaluate:
cosec (65° + A) – sec (25° – A)
A triangle ABC is right angles at B; find the value of`(secA.cosecC - tanA.cotC)/sinB`
Use tables to find cosine of 26° 32’
If 3 cot θ = 4, find the value of \[\frac{4 \cos \theta - \sin \theta}{2 \cos \theta + \sin \theta}\]
If \[\frac{160}{3}\] \[\tan \theta = \frac{a}{b}, \text{ then } \frac{a \sin \theta + b \cos \theta}{a \sin \theta - b \cos \theta}\]
If θ is an acute angle such that \[\tan^2 \theta = \frac{8}{7}\] then the value of \[\frac{\left( 1 + \sin \theta \right) \left( 1 - \sin \theta \right)}{\left( 1 + \cos \theta \right) \left( 1 - \cos \theta \right)}\]
Find the value of the following:
`cot theta/(tan(90^circ - theta)) + (cos(90^circ - theta) tantheta sec(90^circ - theta))/(sin(90^circ - theta)cot(90^circ - theta)"cosec"(90^circ - theta))`
Prove that `"tan A"/"cot A" = (sec^2"A")/("cosec"^2"A")`
The value of the expression (cos2 23° – sin2 67°) is positive.
