Advertisements
Advertisements
प्रश्न
Answer the following:
If f(x) = log(1 – x), 0 ≤ x < 1 show that `"f"(1/(1 + x))` = f(1 – x) – f(– x)
उत्तर
f(x) = log(1 – x)
Replacing x by `(1/(1 + x))`, we get
`"f"(1/(1 + x)) = log(1 - 1/(1 + x))`
= `log((1 + x - 1)/(1 + x))`
= `log(x/(1 + x))`
∴ `"f"(1/(1 + x))` = log x – log(1 + x)
∴ `"f"(1/(1 + x))` = log(1 – 1 + x) – log(1 + x)
∴ `"f"(1/(1 + x))` = log[1 – (1 – x)] – log[1 – (– x)]
∴ `"f"(1/(1 + x))` = f(1 – x) – f(– x)
APPEARS IN
संबंधित प्रश्न
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(b) f2 = {(1, 1), (2, 7), (3, 5)}
If f(x) = x2, find \[\frac{f\left( 1 . 1 \right) - f\left( 1 \right)}{\left( 1 . 1 \right) - 1}\]
If \[f\left( x \right) = \frac{2x}{1 + x^2}\] , show that f(tan θ) = sin 2θ.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
If\[f\left( x \right) = 1 - \frac{1}{x}\] , then write the value of \[f\left( f\left( \frac{1}{x} \right) \right)\]
Write the domain and range of the function \[f\left( x \right) = \frac{x - 2}{2 - x}\] .
Write the domain and range of function f(x) given by
Let f and g be two functions given by
f = {(2, 4), (5, 6), (8, −1), (10, −3)} and g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, −5)}.
Find the domain of f + g
If f(x) = cos (log x), then the value of f(x2) f(y2) −
If 2f (x) − \[3f\left( \frac{1}{x} \right) = x^2\] (x ≠ 0), then f(2) is equal to
If \[f\left( x \right) = 64 x^3 + \frac{1}{x^3}\] and α, β are the roots of \[4x + \frac{1}{x} = 3\] . Then,
The domain of definition of \[f\left( x \right) = \sqrt{\frac{x + 3}{\left( 2 - x \right) \left( x - 5 \right)}}\] is
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
The range of the function \[f\left( x \right) = \frac{x}{\left| x \right|}\] is
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
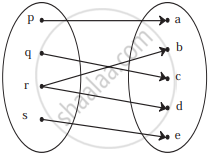
Check if the following relation is function:
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(3)
Which of the following relations are functions? If it is a function determine its domain and range:
{(0, 0), (1, 1), (1, −1), (4, 2), (4, −2), (9, 3), (9, −3), (16, 4), (16, −4)}
Check if the relation given by the equation represents y as function of x:
3x − 6 = 21
If f(m) = m2 − 3m + 1, find `(("f"(2 + "h") - "f"(2))/"h"), "h" ≠ 0`
Find x, if g(x) = 0 where g(x) = `(5x - 6)/7`
Find the domain and range of the following function.
f(x) = `sqrt((x - 2)(5 - x)`
Find the domain and range of the following function.
f(x) = `sqrt((x - 3)/(7 - x))`
Let f be a subset of Z × Z defined by f = {(ab, a + b) : a, b ∈ Z}. Is f a function from Z to Z? Justify?
Express the following exponential equation in logarithmic form
3–4 = `1/81`
Express the following exponential equation in logarithmic form
e2 = 7.3890
Express the following logarithmic equation in exponential form
`log_(1/2) (8)` = – 3
If `log(( x - y)/4) = logsqrt(x) + log sqrt(y)`, show that (x + y)2 = 20xy
Answer the following:
Let f : R – {2} → R be defined by f(x) = `(x^2 - 4)/(x - 2)` and g : R → R be defined by g(x) = x + 2. Examine whether f = g or not
Answer the following:
If `log (("a" + "b")/2) = 1/2(log"a" + log"b")`, then show that a = b
Find the domain of the following function.
f(x) = `sqrtlog(x^2 - 6x + 6)`
A graph representing the function f(x) is given in it is clear that f(9) = 2
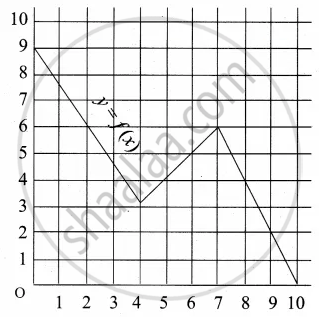
Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
A graph representing the function f(x) is given in it is clear that f(9) = 2
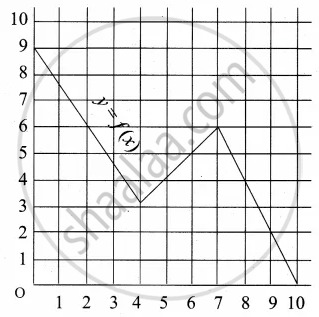
For what value of x is f(x) = 1?
A function f is defined by f(x) = 2x – 3 find x such that f(x) = f(1 – x)
Find the domain of the following function given by:
f(x) = `(3x)/(2x - 8)`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f + g)(x)
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (fg)(x)
The domain for which the functions defined by f(x) = 3x2 – 1 and g(x) = 3 + x are equal is ______.
The domain of f(x) = `sin^-1 [log_2(x/2)]` is ______.
