Advertisements
Advertisements
प्रश्न
The domain of the function \[f\left( x \right) = \sqrt{5 \left| x \right| - x^2 - 6}\] is
पर्याय
(a) (−3, − 2) ∪ (2, 3)
(b) [−3, − 2) ∪ [2, 3)
(c) [−3, − 2] ∪ [2, 3]
(d) None of these
उत्तर
(c) [−3, − 2] ∪ [2, 3]
\[\text{ For f(x) to be defined,} 5\left| x \right| - x^2 - 6 \geq 0\]
\[ \Rightarrow 5\left| x \right| - x^2 - 6 \geq 0\]
\[ \Rightarrow x {}^2 - 5\left| x \right| + 6 \leq 0\]
\[\text{ For } x > 0, \left| x \right| = x\]
\[ \Rightarrow x {}^2 - 5x + 6 \leq 0\]
\[ \Rightarrow (x - 2)(x - 3) \leq 0\]
\[ \Rightarrow x \in [2, 3] . . . . . . . . (1)\]
\[\text{ [For } x < 0, \left| x \right| = - x\]
\[ \Rightarrow x {}^2 + 5x + 6 \leq 0\]
\[ \Rightarrow (x + 2)(x + 3) \leq 0\]
\[ \Rightarrow x \in [ - 3, - 2] . . . . . . . (2)\]
\[\text{ From (1) and (2) } , \]
\[x \in [ - 3, - 2] \cup [2, 3] \]
\[\text{ or, dom } (f) = [ - 3, - 2] \cup [2, 3]\]
APPEARS IN
संबंधित प्रश्न
If f(x) = x2, find `(f(1.1) - f(1))/((1.1 - 1))`
Let f : R → R and g : C → C be two functions defined as f(x) = x2 and g(x) = x2. Are they equal functions?
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(c) f3 = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iv) \[\frac{f}{g}\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iii) \[\frac{f}{g}\]
If f is a real function satisfying \[f\left( x + \frac{1}{x} \right) = x^2 + \frac{1}{x^2}\]
for all x ∈ R − {0}, then write the expression for f(x).
Write the domain and range of function f(x) given by
Let f : R → R be defined by f(x) = 2x + |x|. Then f(2x) + f(−x) − f(x) =
If f : R → R be given by for all \[f\left( x \right) = \frac{4^x}{4^x + 2}\] x ∈ R, then
The domain of the function \[f\left( x \right) = \sqrt{\frac{\left( x + 1 \right) \left( x - 3 \right)}{x - 2}}\] is
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b.
Check if the following relation is a function.
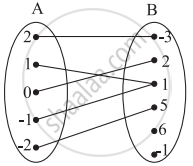
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 2), (2, −1), (3, 1), (4, 3)}
Find the domain and range of the following function.
f(x) = `sqrt(16 - x^2)`
Write the following expression as sum or difference of logarithm
In `(("a"^3 ("a" - 2)^2)/sqrt("b"^2 + 5))`
Select the correct answer from given alternatives.
If log (5x – 9) – log (x + 3) = log 2 then x = ...............
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range
{(12, 1), (3, 1), (5, 2)}
Answer the following:
Find whether the following function is one-one
f : R − {3} → R defined by f(x) = `(5x + 7)/(x - 3)` for x ∈ R − {3}
Answer the following:
Simplify, log (log x4) – log (log x)
Answer the following:
Solve : `sqrt(log_2 x^4) + 4log_4 sqrt(2/x)` = 2
Answer the following:
If `log_2"a"/4 = log_2"b"/6 = log_2"c"/(3"k")` and a3b2c = 1 find the value of k
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - 3) + 1/(log(5 - x))`
Let f = {(x, y) | x, y ∈ N and y = 2x} be a relation on N. Find the domain, co-domain and range. Is this relation a function?
Given the function f: x → x2 – 5x + 6, evaluate f(2a)
Let f(x) = 2x + 5. If x ≠ 0 then find `(f(x + 2) -"f"(2))/x`
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Find the length of forehand of a person if the height is 53.3 inches
If f(x) = `(x - 1)/(x + 1), x ≠ - 1` Show that f(f(x)) = `- 1/x`, Provided x ≠ 0
The range of the function f(x) = `(x^2 - 3x + 2)/(x^3 - 4x^2 + 5x - 2)` is ______
Mapping f: R → R which is defined as f(x) = sin x, x ∈ R will be ______
Find the range of the following functions given by f(x) = `3/(2 - x^2)`
Find the range of the following functions given by f(x) = 1 – |x – 2|
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find `(f/g)(x)`
The range of the function f(x) = `""^(7 - x)P_(x - 3)` is ______.
The domain of f(x) = `sin^-1 [log_2(x/2)]` is ______.
