Advertisements
Advertisements
प्रश्न
The midpoints of the sides of a square of side 1 are joined to form a new square. This procedure is repeated indefinitely. Find the sum of the perimeters of all the squares
उत्तर
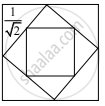
Perimeter of 1st square = 4
Perimeter of 2nd square = `4(1/sqrt(2))`
Perimeter of 3rd square = `4(1/2)`
and so on.
∴ Sum of the perimeters of all the squares
= `4 + 4(1/sqrt(2)) + 4(1/2) + ...`
= `4(1 + 1/sqrt(2) + (1/sqrt(2))^2 + ...)`
The terms `1,1/sqrt(2), (1/sqrt(2))^2, ...` are in G.P.
∴ a = 1, r = `1/sqrt(2)`
Since, |r| = `|1/sqrt(2)| < 1`
∴ sum to infinity exists.
∴ Sum of the perimeters of all the squares
= `4(1/(1 - 1/sqrt(2)))`
= `(4sqrt(2))/(sqrt(2) - 1)`
APPEARS IN
संबंधित प्रश्न
A G.P. consists of an even number of terms. If the sum of all the terms is 5 times the sum of terms occupying odd places, then find its common ratio.
if `(a+ bx)/(a - bx) = (b +cx)/(b - cx) = (c + dx)/(c- dx) (x != 0)` then show that a, b, c and d are in G.P.
Find :
the 12th term of the G.P.
\[\frac{1}{a^3 x^3}, ax, a^5 x^5 , . . .\]
The sum of first three terms of a G.P. is 13/12 and their product is − 1. Find the G.P.
The sum of first three terms of a G.P. is \[\frac{39}{10}\] and their product is 1. Find the common ratio and the terms.
Find three numbers in G.P. whose product is 729 and the sum of their products in pairs is 819.
Find the sum of the following geometric progression:
(a2 − b2), (a − b), \[\left( \frac{a - b}{a + b} \right)\] to n terms;
Find the sum of the following geometric series:
0.15 + 0.015 + 0.0015 + ... to 8 terms;
How many terms of the sequence \[\sqrt{3}, 3, 3\sqrt{3},\] ... must be taken to make the sum \[39 + 13\sqrt{3}\] ?
Prove that: (21/4 . 41/8 . 81/16. 161/32 ... ∞) = 2.
Find an infinite G.P. whose first term is 1 and each term is the sum of all the terms which follow it.
If a, b, c are in G.P., prove that the following is also in G.P.:
a3, b3, c3
If a, b, c are in G.P., then prove that:
Insert 6 geometric means between 27 and \[\frac{1}{81}\] .
Insert 5 geometric means between 16 and \[\frac{1}{4}\] .
If A be one A.M. and p, q be two G.M.'s between two numbers, then 2 A is equal to
Let x be the A.M. and y, z be two G.M.s between two positive numbers. Then, \[\frac{y^3 + z^3}{xyz}\] is equal to
Check whether the following sequence is G.P. If so, write tn.
7, 14, 21, 28, …
The fifth term of a G.P. is x, eighth term of a G.P. is y and eleventh term of a G.P. is z verify whether y2 = xz
The numbers 3, x, and x + 6 form are in G.P. Find 20th term.
Mosquitoes are growing at a rate of 10% a year. If there were 200 mosquitoes in the beginning. Write down the number of mosquitoes after 10 years.
For a G.P. if S5 = 1023 , r = 4, Find a
Find the sum to n terms of the sequence.
0.2, 0.02, 0.002, ...
If S, P, R are the sum, product, and sum of the reciprocals of n terms of a G.P. respectively, then verify that `["S"/"R"]^"n"` = P2
If Sn, S2n, S3n are the sum of n, 2n, 3n terms of a G.P. respectively, then verify that Sn (S3n – S2n) = (S2n – Sn)2.
Express the following recurring decimal as a rational number:
`2.bar(4)`
Express the following recurring decimal as a rational number:
`2.3bar(5)`
The sum of an infinite G.P. is 5 and the sum of the squares of these terms is 15 find the G.P.
Find `sum_("r" = 0)^oo (-8)(-1/2)^"r"`
Select the correct answer from the given alternative.
Which of the following is not true, where A, G, H are the AM, GM, HM of a and b respectively. (a, b > 0)
Answer the following:
Find the nth term of the sequence 0.6, 0.66, 0.666, 0.6666, ...
Answer the following:
If for a G.P. t3 = `1/3`, t6 = `1/81` find r
Answer the following:
If p, q, r, s are in G.P., show that (p2 + q2 + r2) (q2 + r2 + s2) = (pq + qr + rs)2
In a G.P. of positive terms, if any term is equal to the sum of the next two terms. Then the common ratio of the G.P. is ______.
If the pth and qth terms of a G.P. are q and p respectively, show that its (p + q)th term is `(q^p/p^q)^(1/(p - q))`
The third term of G.P. is 4. The product of its first 5 terms is ______.
If in a geometric progression {an}, a1 = 3, an = 96 and Sn = 189, then the value of n is ______.
If the expansion in powers of x of the function `1/((1 - ax)(1 - bx))` is a0 + a1x + a2x2 + a3x3 ....... then an is ______.
