Advertisements
Advertisements
प्रश्न
The midpoints of the sides of a square of side 1 are joined to form a new square. This procedure is repeated indefinitely. Find the sum of the areas of all the squares
उत्तर
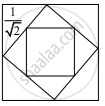
Area of the 1st square = 12
Area of the 2nd square = `(1/sqrt2)^2`
Area of the 3rd square = `(1/2)^2`
and so on
∴ Sum of the areas of all the squares
= `1^2+(1/sqrt2)^2+(1/2)^2+...`
= `1+1/2+1/4+...`
∴ a = 1, r = `1/2`
Since, |r| = `|1/2|<1`
∴ sum to infinity exists.
∴ Sum of the areas of all the squares = `1/(1-1/2)` = 2
APPEARS IN
संबंधित प्रश्न
Which term of the following sequence:
`2, 2sqrt2, 4,.... is 128`
The sum of first three terms of a G.P. is 16 and the sum of the next three terms is 128. Determine the first term, the common ratio and the sum to n terms of the G.P.
If the first and the nth term of a G.P. are a ad b, respectively, and if P is the product of n terms, prove that P2 = (ab)n.
Insert two numbers between 3 and 81 so that the resulting sequence is G.P.
A G.P. consists of an even number of terms. If the sum of all the terms is 5 times the sum of terms occupying odd places, then find its common ratio.
The sum of first three terms of a G.P. is 13/12 and their product is − 1. Find the G.P.
The sum of first three terms of a G.P. is \[\frac{39}{10}\] and their product is 1. Find the common ratio and the terms.
Evaluate the following:
\[\sum^{11}_{n = 1} (2 + 3^n )\]
Find the sum of the following serie:
5 + 55 + 555 + ... to n terms;
The ratio of the sum of first three terms is to that of first 6 terms of a G.P. is 125 : 152. Find the common ratio.
If S1, S2, S3 be respectively the sums of n, 2n, 3n terms of a G.P., then prove that \[S_1^2 + S_2^2\] = S1 (S2 + S3).
Find the sum of 2n terms of the series whose every even term is 'a' times the term before it and every odd term is 'c' times the term before it, the first term being unity.
Find the rational numbers having the following decimal expansion:
\[0 . 6\overline8\]
Show that in an infinite G.P. with common ratio r (|r| < 1), each term bears a constant ratio to the sum of all terms that follow it.
Three numbers are in A.P. and their sum is 15. If 1, 3, 9 be added to them respectively, they form a G.P. Find the numbers.
If a, b, c are in G.P., prove that:
a (b2 + c2) = c (a2 + b2)
If a, b, c, d are in G.P., prove that:
\[\frac{1}{a^2 + b^2}, \frac{1}{b^2 - c^2}, \frac{1}{c^2 + d^2} \text { are in G . P } .\]
If the 4th, 10th and 16th terms of a G.P. are x, y and z respectively. Prove that x, y, z are in G.P.
If pth, qth and rth terms of an A.P. and G.P. are both a, b and c respectively, show that \[a^{b - c} b^{c - a} c^{a - b} = 1\]
Insert 6 geometric means between 27 and \[\frac{1}{81}\] .
Insert 5 geometric means between \[\frac{32}{9}\text{and}\frac{81}{2}\] .
If the fifth term of a G.P. is 2, then write the product of its 9 terms.
The product (32), (32)1/6 (32)1/36 ... to ∞ is equal to
Mark the correct alternative in the following question:
Let S be the sum, P be the product and R be the sum of the reciprocals of 3 terms of a G.P. Then p2R3 : S3 is equal to
If for a sequence, tn = `(5^("n"-3))/(2^("n"-3))`, show that the sequence is a G.P. Find its first term and the common ratio
Mosquitoes are growing at a rate of 10% a year. If there were 200 mosquitoes in the beginning. Write down the number of mosquitoes after 3 years.
For the following G.P.s, find Sn
3, 6, 12, 24, ...
Find: `sum_("r" = 1)^10 5 xx 3^"r"`
Determine whether the sum to infinity of the following G.P.s exist, if exists find them:
`1/2, 1/4, 1/8, 1/16,...`
Find : `sum_("n" = 1)^oo 0.4^"n"`
Select the correct answer from the given alternative.
The tenth term of the geometric sequence `1/4, (-1)/2, 1, -2,` ... is –
Answer the following:
For a G.P. a = `4/3` and t7 = `243/1024`, find the value of r
Answer the following:
Find the nth term of the sequence 0.6, 0.66, 0.666, 0.6666, ...
Answer the following:
Which 2 terms are inserted between 5 and 40 so that the resulting sequence is G.P.
Answer the following:
If a, b, c are in G.P. and ax2 + 2bx + c = 0 and px2 + 2qx + r = 0 have common roots then verify that pb2 – 2qba + ra2 = 0
At the end of each year the value of a certain machine has depreciated by 20% of its value at the beginning of that year. If its initial value was Rs 1250, find the value at the end of 5 years.
Let S be the sum, P be the product and R be the sum of the reciprocals of 3 terms of a G.P. Then P2 R3 : S3 is equal to ______.
The lengths of three unequal edges of a rectangular solid block are in G.P. The volume of the block is 216 cm3 and the total surface area is 252cm2. The length of the longest edge is ______.
