Advertisements
Advertisements
प्रश्न
The midpoints of the sides of a square of side 1 are joined to form a new square. This procedure is repeated indefinitely. Find the sum of the areas of all the squares
उत्तर
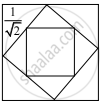
Area of the 1st square = 12
Area of the 2nd square = `(1/sqrt2)^2`
Area of the 3rd square = `(1/2)^2`
and so on
∴ Sum of the areas of all the squares
= `1^2+(1/sqrt2)^2+(1/2)^2+...`
= `1+1/2+1/4+...`
∴ a = 1, r = `1/2`
Since, |r| = `|1/2|<1`
∴ sum to infinity exists.
∴ Sum of the areas of all the squares = `1/(1-1/2)` = 2
APPEARS IN
संबंधित प्रश्न
The 4th term of a G.P. is square of its second term, and the first term is –3. Determine its 7thterm.
Which term of the following sequence:
`2, 2sqrt2, 4,.... is 128`
Find four numbers forming a geometric progression in which third term is greater than the first term by 9, and the second term is greater than the 4th by 18.
The 4th term of a G.P. is square of its second term, and the first term is − 3. Find its 7th term.
If a, b, c, d and p are different real numbers such that:
(a2 + b2 + c2) p2 − 2 (ab + bc + cd) p + (b2 + c2 + d2) ≤ 0, then show that a, b, c and d are in G.P.
Find three numbers in G.P. whose sum is 65 and whose product is 3375.
Find the sum of the following geometric progression:
2, 6, 18, ... to 7 terms;
Evaluate the following:
\[\sum^{10}_{n = 2} 4^n\]
Find the sum of the following series:
7 + 77 + 777 + ... to n terms;
Find the sum of the following series:
0.5 + 0.55 + 0.555 + ... to n terms.
How many terms of the series 2 + 6 + 18 + ... must be taken to make the sum equal to 728?
Find the sum :
\[\sum^{10}_{n = 1} \left[ \left( \frac{1}{2} \right)^{n - 1} + \left( \frac{1}{5} \right)^{n + 1} \right] .\]
Show that the ratio of the sum of first n terms of a G.P. to the sum of terms from (n + 1)th to (2n)th term is \[\frac{1}{r^n}\].
If S1, S2, ..., Sn are the sums of n terms of n G.P.'s whose first term is 1 in each and common ratios are 1, 2, 3, ..., n respectively, then prove that S1 + S2 + 2S3 + 3S4 + ... (n − 1) Sn = 1n + 2n + 3n + ... + nn.
Find the sum of the terms of an infinite decreasing G.P. in which all the terms are positive, the first term is 4, and the difference between the third and fifth term is equal to 32/81.
Find the rational numbers having the following decimal expansion:
\[3 . 5\overline 2\]
One side of an equilateral triangle is 18 cm. The mid-points of its sides are joined to form another triangle whose mid-points, in turn, are joined to form still another triangle. The process is continued indefinitely. Find the sum of the (i) perimeters of all the triangles. (ii) areas of all triangles.
Find an infinite G.P. whose first term is 1 and each term is the sum of all the terms which follow it.
The sum of first two terms of an infinite G.P. is 5 and each term is three times the sum of the succeeding terms. Find the G.P.
Show that in an infinite G.P. with common ratio r (|r| < 1), each term bears a constant ratio to the sum of all terms that follow it.
If a, b, c are in G.P., prove that:
\[\frac{(a + b + c )^2}{a^2 + b^2 + c^2} = \frac{a + b + c}{a - b + c}\]
If a, b, c are in G.P., prove that:
(a + 2b + 2c) (a − 2b + 2c) = a2 + 4c2.
If a, b, c, d are in G.P., prove that:
(a2 + b2), (b2 + c2), (c2 + d2) are in G.P.
If a, b, c are three distinct real numbers in G.P. and a + b + c = xb, then prove that either x< −1 or x > 3.
Insert 6 geometric means between 27 and \[\frac{1}{81}\] .
If pth, qth and rth terms of an A.P. are in G.P., then the common ratio of this G.P. is
The nth term of a G.P. is 128 and the sum of its n terms is 225. If its common ratio is 2, then its first term is
If a, b, c are in G.P. and x, y are AM's between a, b and b,c respectively, then
Check whether the following sequence is G.P. If so, write tn.
`sqrt(5), 1/sqrt(5), 1/(5sqrt(5)), 1/(25sqrt(5))`, ...
For the G.P. if a = `2/3`, t6 = 162, find r.
The numbers 3, x, and x + 6 form are in G.P. Find x
Mosquitoes are growing at a rate of 10% a year. If there were 200 mosquitoes in the beginning. Write down the number of mosquitoes after 10 years.
The numbers x − 6, 2x and x2 are in G.P. Find 1st term
Select the correct answer from the given alternative.
The tenth term of the geometric sequence `1/4, (-1)/2, 1, -2,` ... is –
Answer the following:
Find the nth term of the sequence 0.6, 0.66, 0.666, 0.6666, ...
Answer the following:
Find `sum_("r" = 1)^"n" (2/3)^"r"`
If a, b, c, d are in G.P., prove that a2 – b2, b2 – c2, c2 – d2 are also in G.P.
The lengths of three unequal edges of a rectangular solid block are in G.P. The volume of the block is 216 cm3 and the total surface area is 252cm2. The length of the longest edge is ______.
The sum of the first three terms of a G.P. is S and their product is 27. Then all such S lie in ______.
