Advertisements
Advertisements
प्रश्न
The midpoints of the sides of a square of side 1 are joined to form a new square. This procedure is repeated indefinitely. Find the sum of the perimeters of all the squares
उत्तर
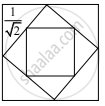
Perimeter of 1st square = 4
Perimeter of 2nd square = `4(1/sqrt(2))`
Perimeter of 3rd square = `4(1/2)`
and so on.
∴ Sum of the perimeters of all the squares
= `4 + 4(1/sqrt(2)) + 4(1/2) + ...`
= `4(1 + 1/sqrt(2) + (1/sqrt(2))^2 + ...)`
The terms `1,1/sqrt(2), (1/sqrt(2))^2, ...` are in G.P.
∴ a = 1, r = `1/sqrt(2)`
Since, |r| = `|1/sqrt(2)| < 1`
∴ sum to infinity exists.
∴ Sum of the perimeters of all the squares
= `4(1/(1 - 1/sqrt(2)))`
= `(4sqrt(2))/(sqrt(2) - 1)`
APPEARS IN
संबंधित प्रश्न
The 5th, 8th and 11th terms of a G.P. are p, q and s, respectively. Show that q2 = ps.
The 4th term of a G.P. is square of its second term, and the first term is –3. Determine its 7thterm.
For what values of x, the numbers `-2/7, x, -7/2` are in G.P?
Evaluate `sum_(k=1)^11 (2+3^k )`
If the first and the nth term of a G.P. are a ad b, respectively, and if P is the product of n terms, prove that P2 = (ab)n.
Find :
the 12th term of the G.P.
\[\frac{1}{a^3 x^3}, ax, a^5 x^5 , . . .\]
Which term of the G.P. :
\[\frac{1}{3}, \frac{1}{9}, \frac{1}{27} . . \text { . is } \frac{1}{19683} ?\]
In a GP the 3rd term is 24 and the 6th term is 192. Find the 10th term.
The sum of first three terms of a G.P. is \[\frac{39}{10}\] and their product is 1. Find the common ratio and the terms.
Find the sum of the following geometric progression:
(a2 − b2), (a − b), \[\left( \frac{a - b}{a + b} \right)\] to n terms;
Find the sum of the following series:
0.6 + 0.66 + 0.666 + .... to n terms
Find the sum :
\[\sum^{10}_{n = 1} \left[ \left( \frac{1}{2} \right)^{n - 1} + \left( \frac{1}{5} \right)^{n + 1} \right] .\]
If S1, S2, ..., Sn are the sums of n terms of n G.P.'s whose first term is 1 in each and common ratios are 1, 2, 3, ..., n respectively, then prove that S1 + S2 + 2S3 + 3S4 + ... (n − 1) Sn = 1n + 2n + 3n + ... + nn.
Prove that: (21/4 . 41/8 . 81/16. 161/32 ... ∞) = 2.
Find k such that k + 9, k − 6 and 4 form three consecutive terms of a G.P.
Three numbers are in A.P. and their sum is 15. If 1, 3, 9 be added to them respectively, they form a G.P. Find the numbers.
If a, b, c are in G.P., prove that:
\[\frac{(a + b + c )^2}{a^2 + b^2 + c^2} = \frac{a + b + c}{a - b + c}\]
If a, b, c, d are in G.P., prove that:
(a + b + c + d)2 = (a + b)2 + 2 (b + c)2 + (c + d)2
If (a − b), (b − c), (c − a) are in G.P., then prove that (a + b + c)2 = 3 (ab + bc + ca)
If the 4th, 10th and 16th terms of a G.P. are x, y and z respectively. Prove that x, y, z are in G.P.
Find the geometric means of the following pairs of number:
a3b and ab3
If logxa, ax/2 and logb x are in G.P., then write the value of x.
If a = 1 + b + b2 + b3 + ... to ∞, then write b in terms of a.
The nth term of a G.P. is 128 and the sum of its n terms is 225. If its common ratio is 2, then its first term is
If p, q be two A.M.'s and G be one G.M. between two numbers, then G2 =
Check whether the following sequence is G.P. If so, write tn.
1, –5, 25, –125 …
Find four numbers in G.P. such that sum of the middle two numbers is `10/3` and their product is 1
The value of a house appreciates 5% per year. How much is the house worth after 6 years if its current worth is ₹ 15 Lac. [Given: (1.05)5 = 1.28, (1.05)6 = 1.34]
If one invests Rs. 10,000 in a bank at a rate of interest 8% per annum, how long does it take to double the money by compound interest? [(1.08)5 = 1.47]
Determine whether the sum to infinity of the following G.P.s exist, if exists find them:
`-3, 1, (-1)/3, 1/9, ...`
A ball is dropped from a height of 10m. It bounces to a height of 6m, then 3.6m and so on. Find the total distance travelled by the ball
Select the correct answer from the given alternative.
Sum to infinity of a G.P. 5, `-5/2, 5/4, -5/8, 5/16,...` is –
Answer the following:
Find `sum_("r" = 1)^"n" (2/3)^"r"`
Answer the following:
Which 2 terms are inserted between 5 and 40 so that the resulting sequence is G.P.
If a, b, c, d are in G.P., prove that a2 – b2, b2 – c2, c2 – d2 are also in G.P.
For a, b, c to be in G.P. the value of `(a - b)/(b - c)` is equal to ______.
The sum of the infinite series `1 + 5/6 + 12/6^2 + 22/6^3 + 35/6^4 + 51/6^5 + 70/6^6 + ....` is equal to ______.
