Question

Find one-parameter families of solution curves of the following differential equation:-

\[\frac{dy}{dx} \cos^2 x = \tan x - y\]

Solve the following differential equation:-

\[\frac{dy}{dx} \cos^2 x = \tan x - y\]

Answer 1

We have,
\[\frac{dy}{dx} \cos^2 x = \tan x - y\]
\[ \Rightarrow \frac{dy}{dx} + \frac{1}{\cos^2 x}y = \tan x \sec^2 x\]
\[ \Rightarrow \frac{dy}{dx} + y \sec^2 x = \tan x \sec^2 x . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dy}{dx} + Py = Q\]
where
\[P = \sec^2 x\]
\[Q = \tan x \sec^2 x\]
\[ \therefore I.F. = e^{\int P\ dx} \]
\[ = e^{\int \sec^2 x\ dx} \]
\[ = e^{\tan x} \]
\[\text{Multiplying both sides of }\left( 1 \right)\text{ by }e^{\tan x} ,\text{ we get }\]
\[ e^{\tan x} \left( \frac{dy}{dx} + y \sec^2 x \right) = e^{\tan x} \tan x \sec^2 x\]
\[ \Rightarrow e^{\tan x} \frac{dy}{dx} + y e^{\tan x} \sec^2 x = e^{\tan x} \tan x \sec^2 x\]
Integrating both sides with respect to x, we get
\[ e^{\tan x} y = \int e^{\tan x} \tan x \sec^2 x dx + C\]
\[ \Rightarrow e^{\tan x} y = I + C . . . . . . . . . . . \left( 2 \right)\]
Where,
\[I = \int e^{\tan x} \tan x \sec^2 x dx\]
\[\text{Putting }t = \tan x,\text{ we get }\]
\[dt = \sec^2 x dx\]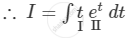

\[ = t\int e^t dt - \int\left[ \frac{d}{dt}\left( t \right)\int e^t dt \right]dt\]
\[ = t e^t - e^t \]
\[ = \left( t - 1 \right) e^t \]
\[ = \left( \tan x - 1 \right) e^{\tan x} \]
\[\text{ Putting the value of I in }\left( 2 \right),\text{ we get }\]
\[ e^{\tan x} y = \left( \tan x - 1 \right) e^{\tan x} + C\]
\[ \Rightarrow y = \left( \tan x - 1 \right) + C e^{- \tan x} \]
\[\text{ Hence, }y = \left( \tan x - 1 \right) + C e^{- \tan x} \text{ is the required solution.}\]