Advertisements
Advertisements
प्रश्न
if `x^m y^n = (x + y)^(m + n)`, prove that `(d^2y)/(dx^2)= 0`
उत्तर
We are given
`x^m y^n = (x + y)^(m + n)`
Taking log on both sides, we get
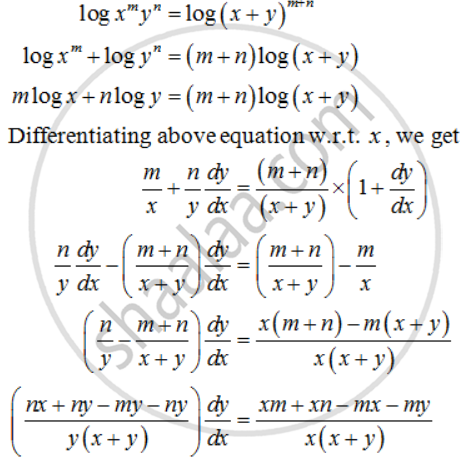

APPEARS IN
संबंधित प्रश्न
Differentiate the function with respect to x.
(x + 3)2 . (x + 4)3 . (x + 5)4
Differentiate the function with respect to x.
(log x)x + xlog x
Differentiate the function with respect to x.
`x^(xcosx) + (x^2 + 1)/(x^2 -1)`
Differentiate the function with respect to x.
`(x cos x)^x + (x sin x)^(1/x)`
Find `dy/dx` for the function given in the question:
yx = xy
Find `dy/dx` for the function given in the question:
(cos x)y = (cos y)x
Find the derivative of the function given by f (x) = (1 + x) (1 + x2) (1 + x4) (1 + x8) and hence find f ′(1).
If `y = sin^-1 x + cos^-1 x , "find" dy/dx`
Evaluate
`int 1/(16 - 9x^2) dx`
Find `dy/dx` if y = xx + 5x
Differentiate
log (1 + x2) w.r.t. tan-1 (x)
Find `(d^2y)/(dx^2)` , if y = log x
If ey = yx, then show that `"dy"/"dx" = (logy)^2/(log y - 1)`.
If x = sin–1(et), y = `sqrt(1 - e^(2t)), "show that" sin x + dy/dx` = 0
If y = log (log 2x), show that xy2 + y1 (1 + xy1) = 0.
Choose the correct option from the given alternatives :
If xy = yx, then `"dy"/"dx"` = ..........
If x7 . y5 = (x + y)12, show that `("d"y)/("d"x) = y/x`
If xy = ex-y, then `"dy"/"dx"` at x = 1 is ______.
`d/dx(x^{sinx})` = ______
If y = `("e"^"2x" sin x)/(x cos x), "then" "dy"/"dx" = ?`
Derivative of `log_6`x with respect 6x to is ______
`log (x + sqrt(x^2 + "a"))`
If xm . yn = (x + y)m+n, prove that `"dy"/"dx" = y/x`
If `"y" = "e"^(1/2log (1 + "tan"^2"x")), "then" "dy"/"dx"` is equal to ____________.
Given f(x) = `log((1 + x)/(1 - x))` and g(x) = `(3x + x^3)/(1 + 3x^2)`, then fog(x) equals
If y = `x^(x^2)`, then `dy/dx` is equal to ______.
If y = `log(x + sqrt(x^2 + 4))`, show that `dy/dx = 1/sqrt(x^2 + 4)`
Evaluate:
`int log x dx`
