Advertisements
Advertisements
Question
if `x^m y^n = (x + y)^(m + n)`, prove that `(d^2y)/(dx^2)= 0`
Solution
We are given
`x^m y^n = (x + y)^(m + n)`
Taking log on both sides, we get
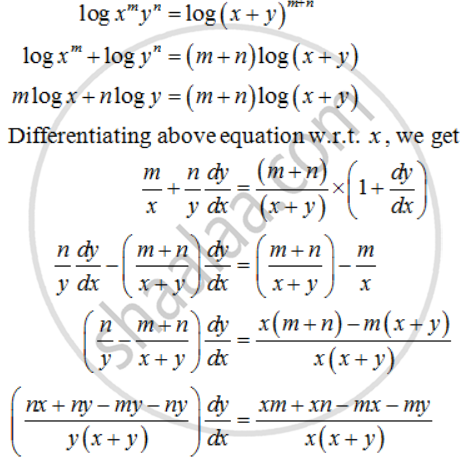

APPEARS IN
RELATED QUESTIONS
Differentiate the function with respect to x.
(x + 3)2 . (x + 4)3 . (x + 5)4
Differentiate the function with respect to x.
xsin x + (sin x)cos x
Differentiate the function with respect to x.
`x^(xcosx) + (x^2 + 1)/(x^2 -1)`
Find `dy/dx` for the function given in the question:
`xy = e^((x – y))`
Find the derivative of the function given by f (x) = (1 + x) (1 + x2) (1 + x4) (1 + x8) and hence find f ′(1).
If cos y = x cos (a + y), with cos a ≠ ± 1, prove that `dy/dx = cos^2(a+y)/(sin a)`
If `y = sin^-1 x + cos^-1 x , "find" dy/dx`
Evaluate
`int 1/(16 - 9x^2) dx`
If y = (log x)x + xlog x, find `"dy"/"dx".`
If log (x + y) = log(xy) + p, where p is a constant, then prove that `"dy"/"dx" = (-y^2)/(x^2)`.
If xy = ex–y, then show that `"dy"/"dx" = logx/(1 + logx)^2`.
If x = `asqrt(secθ - tanθ), y = asqrt(secθ + tanθ), "then show that" "dy"/"dx" = -y/x`.
If x = log(1 + t2), y = t – tan–1t,show that `"dy"/"dx" = sqrt(e^x - 1)/(2)`.
If x = `(2bt)/(1 + t^2), y = a((1 - t^2)/(1 + t^2)), "show that" "dx"/"dy" = -(b^2y)/(a^2x)`.
Find the second order derivatives of the following : log(logx)
If f(x) = logx (log x) then f'(e) is ______
If log5 `((x^4 + "y"^4)/(x^4 - "y"^4))` = 2, show that `("dy")/("d"x) = (12x^3)/(13"y"^2)`
If y = `{f(x)}^{phi(x)}`, then `dy/dx` is ______
If y = `("e"^"2x" sin x)/(x cos x), "then" "dy"/"dx" = ?`
Derivative of `log_6`x with respect 6x to is ______
`8^x/x^8`
`log (x + sqrt(x^2 + "a"))`
`lim_("x" -> -2) sqrt ("x"^2 + 5 - 3)/("x" + 2)` is equal to ____________.
If `"f" ("x") = sqrt (1 + "cos"^2 ("x"^2)), "then the value of f'" (sqrtpi/2)` is ____________.
If `"y" = "e"^(1/2log (1 + "tan"^2"x")), "then" "dy"/"dx"` is equal to ____________.
If y = `x^(x^2)`, then `dy/dx` is equal to ______.
Find `dy/dx`, if y = (sin x)tan x – xlog x.
The derivative of log x with respect to `1/x` is ______.
