Advertisements
Chapters
![NCERT solutions for Mathematics [English] Class 9 chapter 1 - Number Systems NCERT solutions for Mathematics [English] Class 9 chapter 1 - Number Systems - Shaalaa.com](/images/mathematics-english-class-9_6:e75a1668572245b2974a4e6dc62140a3.jpg)
Advertisements
Solutions for Chapter 1: Number Systems
Below listed, you can find solutions for Chapter 1 of CBSE NCERT for Mathematics [English] Class 9.
NCERT solutions for Mathematics [English] Class 9 1 Number Systems EXERCISE 1.1 [Page 5]
Is zero a rational number? Can you write it in the form `p/q`, where p and q are integers and q ≠ 0?
Find six rational numbers between 3 and 4.
Find five rational numbers between `3/5` and `4/5`.
State whether the following statement is true or false. Give reasons for your answer.
Every natural number is a whole number.
True
False
State whether the following statement is true or false. Give reasons for your answer.
Every integer is a whole number.
True
False
State whether the following statement is true or false. Give reasons for your answer.
Every rational number is a whole number.
True
False
NCERT solutions for Mathematics [English] Class 9 1 Number Systems EXERCISE 1.2 [Page 8]
State whether the following statement is true or false. Justify your answer.
Every irrational number is a real number.
True
False
State whether the following statement is true or false. Justify your answer.
Every point on the number line is of the form `sqrt m`, where m is a natural number.
True
False
State whether the following statement is true or false. Justify your answer.
Every real number is an irrational number.
True
False
Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Show how `sqrt5` can be represented on the number line.
Classroom activity (Constructing the ‘square root spiral’): Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP1 of unit length. Draw a line segment P1 P2 perpendicular to OP1 of unit length. Now draw a line segment P2 P3 perpendicular to OP2. Then draw a line segment P3 P4 perpendicular to OP3. Continuing in this manner, you can get the line segment Pn–1Pn by drawing a line segment of unit length perpendicular to OPn–1. In this manner, you will have created the points P2, P3,...., Pn,.... ., and joined them to create a beautiful spiral depicting `sqrt2, sqrt3, sqrt4,` ...
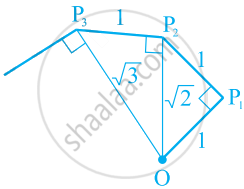
NCERT solutions for Mathematics [English] Class 9 1 Number Systems EXERCISE 1.3 [Page 14]
Write the following in decimal form and say what kind of decimal expansion has:
`36/100`
Write the following in decimal form and say what kind of decimal expansion has:
`1/11`
Write the following in decimal form and say what kind of decimal expansion has:
`4 1/8`
Write the following in decimal form and say what kind of decimal expansion has:
`3/13`
Write the following in decimal form and say what kind of decimal expansion has:
`2/11`
Write the following in decimal form and say what kind of decimal expansion has:
`329/400`
You know that `1/7=0.bar142857.` Can you predict what the decimal expansions of `2/7, 3/7, 4/7, 5/7, 6/7` are, Without actually doing the long division? If so, how?
[Hint: Study the remainders while finding the value of `1/7` carefully.]
Express the following in the form `p/q`, where p and q are integers and q ≠ 0.
`0.bar6`
Express the following in the form `bb(p/q)`, where p and q are integers and q ≠ 0.
`0.4bar7`
Express the following in the form `bb(p/q)`, where p and q are integers and q ≠ 0.
`0.bar001`
Express 0.99999 .... in the form `p/q`. Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
What can the maximum number of digits be in the repeating block of digits in the decimal expansion of `1/17`? Perform the division to check your answer.
Look at several examples of rational numbers in the form `p/q` (q≠0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Write three numbers whose decimal expansions are non-terminating non-recurring.
Find three different irrational numbers between the rational numbers `5/7` and `9/11.`
Classify the following number as rational or irrational:
`sqrt23`
Classify the following number as rational or irrational:
`sqrt225`
Classify the following number as rational or irrational:
0.3796
Classify the following number as rational or irrational:
7.478478...
Classify the following number as rational or irrational:
1.101001000100001...
NCERT solutions for Mathematics [English] Class 9 1 Number Systems EXERCISE 1.4 [Pages 20 - 21]
Classify the following numbers as rational or irrational:
`2-sqrt5`
Classify the following number as rational or irrational:
`(3+sqrt23)-sqrt23`
Classify the following number as rational or irrational:
`(2sqrt7)/(7sqrt7)`
Classify the following number as rational or irrational:
`1/sqrt2`
Classify the following number as rational or irrational:
2π
Simplify the following expression:
`(3+sqrt3)(2+sqrt2)`
Simplify the following expression:
`(3+sqrt3)(3-sqrt3)`
Simplify the following expression:
`(sqrt5+sqrt2)^2`
Simplify the following expression:
`(sqrt5-sqrt2)(sqrt5+sqrt2)`
Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π = `c/d`. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?
Represent `sqrt9.3` on the number line.
Rationalise the denominator of the following:
`1/sqrt7`
Rationalise the denominator of the following:
`1/(sqrt7-sqrt6)`
Rationalise the denominator of the following:
`1/(sqrt5+sqrt2)`
Rationalise the denominator of the following:
`1/(sqrt7-2)`
NCERT solutions for Mathematics [English] Class 9 1 Number Systems EXERCISE 1.5 [Page 23]
Find:-
`64^(1/2)`
Find:-
`32^(1/5)`
Find:-
`125^(1/3)`
Find:-
`9^(3/2)`
Find:-
`32^(2/5)`
Find:-
`16^(3/4)`
Find:-
`125^((-1)/3)`
Simplify:-
`2^(2/3). 2^(1/5)`
Simplify:-
`(1/3^3)^7`
Simplify:
`11^(1/2)/11^(1/4)`
Simplify:
`7^(1/2) . 8^(1/2)`
Solutions for 1: Number Systems
![NCERT solutions for Mathematics [English] Class 9 chapter 1 - Number Systems NCERT solutions for Mathematics [English] Class 9 chapter 1 - Number Systems - Shaalaa.com](/images/mathematics-english-class-9_6:e75a1668572245b2974a4e6dc62140a3.jpg)
NCERT solutions for Mathematics [English] Class 9 chapter 1 - Number Systems
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 9 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT solutions for Mathematics Mathematics [English] Class 9 CBSE 1 (Number Systems) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 9 chapter 1 Number Systems are Introduction of Real Number, Concept of Irrational Numbers, Real Numbers and Their Decimal Expansions, Representing Real Numbers on the Number Line, Operations on Real Numbers, Laws of Exponents for Real Numbers, Introduction of Real Number, Concept of Irrational Numbers, Real Numbers and Their Decimal Expansions, Representing Real Numbers on the Number Line, Operations on Real Numbers, Laws of Exponents for Real Numbers.
Using NCERT Mathematics [English] Class 9 solutions Number Systems exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 9 students prefer NCERT Textbook Solutions to score more in exams.
Get the free view of Chapter 1, Number Systems Mathematics [English] Class 9 additional questions for Mathematics Mathematics [English] Class 9 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
