Advertisements
Chapters
2: वर्गसमीकरण
3: अंकगणितीय श्रृंखला
4: आर्थिक नियोजन
5: संभाव्यता
6: सांख्यिकी
![Balbharati solutions for Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board chapter 1 - दो चरांकों वाले रेखीय समीकरण Balbharati solutions for Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board chapter 1 - दो चरांकों वाले रेखीय समीकरण - Shaalaa.com](/images/algebra-mathematics-1-hindi-10-standard-ssc-maharashtra-state-board_6:cbb956991fdf4eb99c661d02278d18ad.jpg)
Advertisements
Solutions for Chapter 1: दो चरांकों वाले रेखीय समीकरण
Below listed, you can find solutions for Chapter 1 of Maharashtra State Board Balbharati for Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board.
Balbharati solutions for Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board 1 दो चरांकों वाले रेखीय समीकरण प्रश्नसंग्रह 1.1 [Pages 4 - 5]
निम्न कृति पूर्ण करके युगपत समीकरण हल कीजिए।
5x + 3y = 9 ......(I)
2x − 3y = 12 ......(II)
समीकरण (I) तथा समीकरण (II) को जोड़ने पर
5x + 3y = 9
+ 2x − 3y = 12
`square` x = `square`
x = `square/square` x = `square`
x = 3 समीकरण (I) मेंं रखने पर -
5 × `square` + 3y = 9
3y = 9 − `square`
3y = `square`
y = `square/3`
y = `square`
(x, y) = `(square, square)` समीकरण का हल है।
निम्न युगपत समीकरण को हल कीजिए।
3a + 5b = 26; a + 5b = 22
निम्न युगपत समीकरण को हल कीजिए।
x + 7y = 10; 3x − 2y = 7
निम्न युगपत समीकरण को हल कीजिए।
2x − 3y = 9; 2x + y = 13
निम्न युगपत समीकरण को हल कीजिए।
5m − 3n = 19; m − 6n = −7
निम्न युगपत समीकरण को हल कीजिए।
5x + 2y = −3; x + 5y = 4
निम्न युगपत समीकरण को हल कीजिए।
`1/3 "x" + "y" = 10/3`; `2"x" + 1/4"y" = 11/4`
निम्न युगपत समीकरण को हल कीजिए।
99x + 101y = 499; 101x + 99y = 501
निम्न युगपत समीकरण को हल कीजिए।
49x − 57y = 172; 57x − 49y = 252
Balbharati solutions for Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board 1 दो चरांकों वाले रेखीय समीकरण प्रश्नसंग्रह 1.2 [Page 8]
निम्नलिखित युगपत समीकरण आलेख विधि से हल करने के लिए सारिणी पूर्ण कीजिए।
x + y = 3
| x | 3 | `square` | `square` |
| y | `square` | 5 | 3 |
| (x, y) | (3, 0) | `square` | (0, 3) |
निम्नलिखित युगपत समीकरण आलेख विधि से हल करने के लिए सारिणी पूर्ण कीजिए।
x − y = 4
| x | `square` | −1 | 0 |
| y | 0 | `square` | −4 |
| (x, y) | `square` | `square` | (0, −4) |
निम्नलिखित युगपत समीकरण आलेख विधि से हल कीजिए।
x + y = 6; x − y = 4
निम्नलिखित युगपत समीकरण आलेख विधि से हल कीजिए।
x + y = 5; x − y = 3
निम्नलिखित युगपत समीकरण आलेख विधि से हल कीजिए।
x + y = 0; 2x − y = 9
निम्नलिखित युगपत समीकरण आलेख विधि से हल कीजिए।
3x − y = 2; 2x − y = 3
निम्नलिखित युगपत समीकरण आलेख विधि से हल कीजिए।
3x − 4y = −7; 5x − 2y = 0
निम्नलिखित युगपत समीकरण आलेख विधि से हल कीजिए।
2x − 3y = 4; 3y − x = 4
Balbharati solutions for Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board 1 दो चरांकों वाले रेखीय समीकरण प्रश्नसंग्रह 1.3 [Page 16]
`|(3,2),(4,5)| = 3 xx square - square xx 4 = square - 8 = square`
निम्नलिखित निश्चयकों का मान ज्ञात कीजिए।
`|(-1, 7), (2, 4)|`
निम्नलिखित निश्चयकों का मान ज्ञात कीजिए।
`|(5, 3), (-7, 0)|`
निम्नलिखित निश्चयकों का मान ज्ञात कीजिए।
`|(7/3, 5/3), (3/2, 1/2)|`
निम्नलिखित युगपत समीकरणों को क्रेमर की पद्धति से हल कीजिए।
3x − 4y = 10; 4x + 3y = 5
निम्नलिखित युगपत समीकरणों को क्रेमर की पद्धति से हल कीजिए।
4x + 3y − 4 = 0; 6x = 8 − 5y
निम्नलिखित युगपत समीकरणों को क्रेमर की पद्धति से हल कीजिए।
x + 2y = − 1; 2x − 3y = 12
निम्नलिखित युगपत समीकरणों को क्रेमर की पद्धति से हल कीजिए।
6x − 4y = − 12; 8x − 3y = − 2
निम्नलिखित युगपत समीकरणों को क्रेमर की पद्धति से हल कीजिए।
4m + 6n = 54; 3m + 2n = 28
निम्नलिखित युगपत समीकरणों को क्रेमर की पद्धति से हल कीजिए।
2x + 3y = 2; `"x" - "y"/2 = 1/2`
Balbharati solutions for Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board 1 दो चरांकों वाले रेखीय समीकरण प्रश्नसंग्रह 1.4 [Page 19]
निम्नलिखित युगपत समीकरणों को हल कीजिए।
`2/"x" - 3/"y" = 15; 8/"x" + 5/"y" = 77`
निम्नलिखित युगपत समीकरणों को हल कीजिए।
`10/("x" + "y") + 2/("x" - "y") = 4; 15/("x" + "y") - 5/("x" - "y") = -2`
निम्नलिखित युगपत समीकरणों को हल कीजिए।
`27/("x" - 2) + 31/("y" + 3) = 85; 31/("x" - 2) + 27/("y" + 3) = 89`
निम्नलिखित युगपत समीकरणों को हल कीजिए।
`1/(3"x" + "y") + 1/(3"x" - "y") = 3/4; 1/(2(3"x" + "y")) - 1/(2(3"x" - "y")) = -1/8`
Balbharati solutions for Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board 1 दो चरांकों वाले रेखीय समीकरण प्रश्नसंग्रह 1.5 [Page 26]
दो संख्याओं का अंतर 3 है। बड़ी संख्या का तीन गुना और छोटी संख्या के दुगुने का योगफल 19 हो तो वह संख्या ज्ञात कीजिए।
कृति पूर्ण कीजिए।
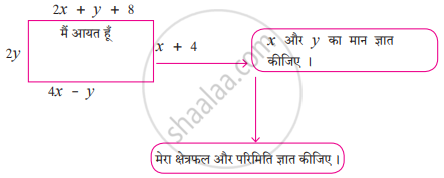
पिता की आयु मेंं पुत्र की आयु का दुगुना जोड़ने पर योगफल 70 प्राप्त होता है और पुत्र की आयु मेंं पिता की आयु का दुगुना जोड़ने पर 95 प्राप्त होता है तो दोनों की वर्तमान आयु ज्ञात कीजिए।
किसी भिन्न का हर उसके अंश के दुगुने से 4 अधिक है। अंश और हर दोनों मेंं से 6 घटाने पर हर, अंश का 12 गुना होता है तो वह भिन्न ज्ञात कीजिए।
10 टन क्षमतावाले मालवाहक ट्रक मेंं A और B ऐसे दो प्रकार के बक्से भरे हैं। यदि A प्रकार के 150 बक्से तथा B प्रकार के 100 बक्से भरे हैं तो ट्रक की 10 टन की क्षमता पूर्ण होती है। यदि A प्रकार के 260 बक्से भरें तब उस ट्रक की 10 टन क्षमता को पूर्ण करने के लिए B प्रकार के 40 बक्से लगते हैं, तो प्रत्येक प्रकार के बक्सों का भार ज्ञात कीजिए।
विशाल ने 1900 किमी के सफर मेंं कुछ दूरी बस से और कुछ दूरी हवाई जहाज से पूरी की। बस का औसत वेग 60 किमी/घंटा है तथा हवाई जहाज का औसत वेग 700 किमी/घंटा है। यदि इस सफर को उसने 5 घंटे मेंं पूरा किया हो तो विशाल ने बस से कितने किमी सफर तय किया?
Balbharati solutions for Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board 1 दो चरांकों वाले रेखीय समीकरण प्रकीर्ण प्रश्नसंग्रह 1 [Pages 27 - 29]
निम्नलिखित प्रश्नों के लिए दिए गए विकल्पों मेंं से उचित विकल्प को चुनिए।
4x + 5y = 19 का आलेख खींचने के लिए x = 1 हो तो y का मान ज्ञात कीजिए।
4
3
2
− 3
x तथा y चरांक वाले युगपत समीकरण के लिए यदि Dx = 49, Dy = − 63 तथा D = 7 हो तो x = कितना?
7
− 7
`1/7`
`(-1)/7`
`|(5,3),(-7,-4)|` इस निश्चयक का मान ज्ञात कीजिए।
− 1
− 41
41
1
x + y = 3; 3x − 2y − 4 = 0 इस युगपत समीकरण को हल करने के लिए D का मान कितना होगा?
5
1
− 5
− 1
ax + by = c; तथा mx + ny = d इस युगपत समीकरण मेंं यदि an ≠ bm तो दिए गए समीकरण का
एक ही हल होगा।
हल नहीं होगा।
असंख्य हल होंगे।
सिर्फ दो हल होंगे।
2x − 6y = 3 इस समीकरण का आलेख खींचने के लिए सारिणी पूर्ण कीजिए।
| x | −5 | `square` |
| y | `square` | 0 |
| (x, y) | `square` | `square` |
निम्नलिखित युगपत समीकरणों को आलेख विधि से हल कीजिए।
2x + 3y = 12; x − y = 1
निम्नलिखित युगपत समीकरणों को आलेख विधि से हल कीजिए।
x − 3y = 1; 3x − 2y + 4 = 0
निम्नलिखित युगपत समीकरणों को आलेख विधि से हल कीजिए।
5x − 6y + 30 = 0; 5x + 4y − 20 = 0
निम्नलिखित युगपत समीकरणों को आलेख विधि से हल कीजिए।
3x − y − 2 = 0; 2x + y = 8
निम्नलिखित युगपत समीकरणों को आलेख विधि से हल कीजिए।
3x + y = 10; x − y = 2
निम्नलिखित निश्चयकों का मान ज्ञात कीजिए।
`|(4, 3), (2, 7)|`
निम्नलिखित निश्चयकों का मान ज्ञात कीजिए।
`|(5, -2), (-3, 1)|`
निम्नलिखित निश्चयकों का मान ज्ञात कीजिए।
`|(3, -1), (1, 4)|`
निम्नलिखित युगपत समीकरणों को क्रेमर की पद्धति से हल कीजिए।
6x − 3y = − 10; 3x + 5y − 8 = 0
निम्नलिखित युगपत समीकरणों को क्रेमर की पद्धति से हल कीजिए।
4m − 2n = − 4; 4m + 3n = 16
निम्नलिखित युगपत समीकरणों को क्रेमर की पद्धति से हल कीजिए।
3x − 2y = `5/2`; `1/3`x + 3y = `-4/3`
निम्नलिखित युगपत समीकरणों को क्रेमर की पद्धति से हल कीजिए।
7x + 3y = 15; 12y − 5x = 39
निम्नलिखित युगपत समीकरणों को क्रेमर की पद्धति से हल कीजिए।
`("x" + "y" - 8)/2 = ("x" + 2"y" - 14)/3 = (3"x" - "y")/4`
निम्नलिखित युगपत समीकरण हल कीजिए।
`2/"x" + 2/(3"y") = 1/6; 3/"x" + 2/"y" = 0`
निम्नलिखित युगपत समीकरण हल कीजिए।
`7/(2"x" + 1) + 13/("y" + 2) = 27; 13/(2"x" + 1) + 7/("y" + 2) = 33`
निम्नलिखित युगपत समीकरण हल कीजिए।
`148/"x" + 231/"y" = 527/"xy"; 231/"x" + 148/"y" = 610/"xy"`
निम्नलिखित युगपत समीकरण हल कीजिए।
`(7"x" - 2"y")/"xy" = 5; (8"x" + 7"y")/"xy" = 15`
निम्नलिखित युगपत समीकरण हल कीजिए।
`1/(2(3"x" + 4"y")) + 1/(5(2"x" - 3"y")) = 1/4; 5/((3"x" + 4"y")) - 2/((2"x" - 3"y")) = -3/2`
निम्नलिखित प्रश्न हल कीजिए।
किसी दो अंकोंवाली संख्या मेंं उसके अंकों का स्थान परस्पर बदलने पर प्राप्त संख्या को जोड़ने पर योगफल 143 आता है। यदि दी गई संख्या के इकाई के स्थान का अंक, दहाई स्थान के अंक से 3 अधिक हो तो दी गई मूल संख्या कौन-सी है? उत्तर ज्ञात करने के लिए निम्नलिखित कृति पूर्ण कीजिए।
माना इकाई स्थान का अंक = x
दहाई स्थान का अंक = y
∴ मूल संख्या = `square` y + x
अंकों के परस्पर स्थान परिवर्तन से प्राप्त संख्या = `square` x + y
प्रथम शर्त के अनुसार: दो अंकोंवाली संख्या + अंकों के स्थान परिवर्तन से प्राप्त संख्या = 143
10x + y + `square` = 143
`square` x + `square` y = 143
x + y = `square` ...........(I)
दूसरी शर्त के अनुसार,
इकाई स्थान का अंक = दहाई स्थान का अंक + 3
x = `square` + 3
∴ x − y = 3 .................(II)
(I) तथा (II) को जोड़ने पर
2x = `square`
∴ x = 8
x = 8 समीकरण (I) मेंं रखने पर
x + y = 13
8 + `square` = 13
y = `square`
मूल संख्या = 10 y + x
= `square` + 8 = 58
कांताबेन ने दुकान से डेढ़ किलो चाय की पत्ती तथा पाँच किलो शक्कर खरीदी। दुकान जाने-आने के लिए उन्हें रिक्शा का किराया 50 रूपये देना पड़ा। ऐसे कुल 700 रूपये खर्च हुए। बाद मेंं उन्हें समझ में आया कि यह वस्तुएँ ऑनलाइन ऑर्डर देकर भी उसी दर पर ही घर पहुँच मिलती हैं। अगले महीने उन्होंने 2 किलोग्राम चाय की पत्ती तथा 7 किलोग्राम शक्कर ऑनलाईन मँगवाई तब उन्होंने 880 रूपये खर्च किए। चाय की पत्ती और शक्कर का प्रति किलोग्राम दर ज्ञात कीजिए।
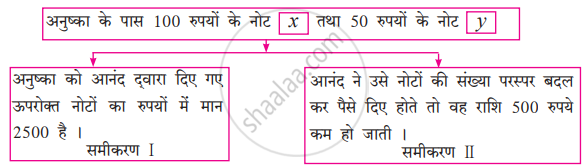
समीकरण हल करके उत्तर लिखिए।
100 रुपये के नोटों की संख्या `square`, 50 रूपये के नोटों की संख्या `square`
मनीषा और सविता की वर्तमान आयु का योगफल 31 वर्ष है। 3 वर्ष पूर्व मनीष की आयु सविता की उस समय की आयु की चौगुनी थी, तो दोनों की वर्तमान आयु ज्ञात करो।
एक कारखाने मेंं कुशल और अकुशल मजदूरों की मजदूरी का अनुपात 5 : 3 है। एक कुशल और एक अकुशल मजदूर के एक दिन की कुल मजदूरी 720 रूपये है। तो प्रत्येक कुशल मजदूर और अकुशल मजदूरों की मजदूरी ज्ञात कीजिए।
एक सीधे रास्ते पर A और B दो स्थान हैं। उनके बीच दूरी 30 किमी है। हमीद मोटरसाइकिल से A से B दिशा जाने के लिए निकलता है। उसी समय जोसफ B से A की दिशा मेंं जाने के लिए निकलता है वे दोनों 20 मिनट मेंं एक-दूसरे से मिलते हैं। यदि उसी समय जोसेफ निकलकर विपरीत दिशा मेंं गया होता, तो उसे हमीद तीन घंटे बाद मिलता तो प्रत्येक की गति ज्ञात कीजिए।
Solutions for 1: दो चरांकों वाले रेखीय समीकरण
![Balbharati solutions for Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board chapter 1 - दो चरांकों वाले रेखीय समीकरण Balbharati solutions for Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board chapter 1 - दो चरांकों वाले रेखीय समीकरण - Shaalaa.com](/images/algebra-mathematics-1-hindi-10-standard-ssc-maharashtra-state-board_6:cbb956991fdf4eb99c661d02278d18ad.jpg)
Balbharati solutions for Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board chapter 1 - दो चरांकों वाले रेखीय समीकरण
Shaalaa.com has the Maharashtra State Board Mathematics Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board Maharashtra State Board solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Balbharati solutions for Mathematics Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board Maharashtra State Board 1 (दो चरांकों वाले रेखीय समीकरण) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Balbharati textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board chapter 1 दो चरांकों वाले रेखीय समीकरण are दो चरांकों वाले रेखीय समीकरणे, युगपत रेखीय समीकरण (Simultaneous Linear Equations), दो चरांकों वाले रेखीय समीकरणों का आलेख (Graph of Linear Equation in Two Variables), युगपत समीकरण हल करन की आलेख विधि (Solution of Simultaneous Equation by Graphical Method), निश्चयक (Determinant), निशच्यक पद्धति (क्रेमर की पद्धति) Determinant Method (Crammer’s Method), दो चरांकों वाले रेखीय समीकरण मेंं रूपांतर करने योग्य समीकरण (Equations Reducible to a Pair of Linear Equations in Two Variables), युगपत समीकरण पर आधारित शाब्दिक उदाहरणे.
Using Balbharati Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board solutions दो चरांकों वाले रेखीय समीकरण exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Balbharati Solutions are essential questions that can be asked in the final exam. Maximum Maharashtra State Board Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board students prefer Balbharati Textbook Solutions to score more in exams.
Get the free view of Chapter 1, दो चरांकों वाले रेखीय समीकरण Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board additional questions for Mathematics Algebra (Mathematics 1) [Hindi] 10 Standard SSC Maharashtra State Board Maharashtra State Board, and you can use Shaalaa.com to keep it handy for your exam preparation.
