Advertisements
Advertisements
Question
`(5/7, (2sqrt(6))/7)` is a point on the terminal side of an angle θ in standard position. Determine the six trigonometric function values of angle θ
Solution
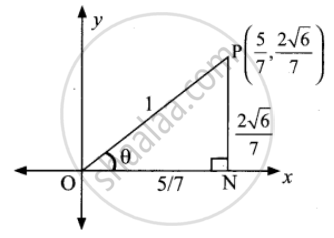
In the diagram ON = `5/7`
PN = `(2sqrt(6))/7`
ON2 + NP2 = OP2
(i.e) `25/49 + 24/49 = 49/49` = OP2
⇒ OP = 1
sin θ = `"PN"/"OP"`
= `(2sqrt(6)/7)/1`
= `(2sqrt(6))/7`
cos θ = `"ON"/"OP"`
= `(5/7)/1`
= `5/7`
tan θ = `"PN"/"ON"`
= `((2sqrt(6))/7)/(5/7)`
= `(2sqrt(6))/5`
cosec θ = `1/sintheta = 7/(2sqrt(6))`
sec θ = `1/costheta = 7/5`
cot θ = `1/tantheta = 5/(2sqrt(6))`
APPEARS IN
RELATED QUESTIONS
Find the value of the trigonometric functions for the following:
cos θ = `- 2/3`, θ lies in the IV quadrant
Prove that `(cot(180^circ + theta) sin(90^circ - theta) cos(- theta))/(sin(270^circ + theta) tan(- theta) "cosec"(360^circ + theta))` = cos2θ cotθ
Prove that sin(30° + θ) + cos(60° + θ) = cos θ
Prove that cos(A + B) cos C – cos(B + C) cos A = sin B sin(C – A)
If x cos θ = `y cos (theta + (2pi)/3) = z cos (theta + (4pi)/3)`. find the value of xy + yz + zx
Prove that sin(A + B) sin(A – B) = sin2A – sin2B
Prove that cos(A + B) cos(A – B) = cos2A – sin2B = cos2B – sin2A
If cos θ = `1/2 ("a" + 1/"a")`, show that cos 3θ = `1/2 ("a"^3 + 1/"a"^3)`
Prove that sin 4α = `4 tan alpha (1 - tan^2alpha)/(1 + tan^2 alpha)^2`
Show that `cot(7 1^circ/2) = sqrt(2) + sqrt(3) + sqrt(4) + sqrt(6)`
Prove that `32(sqrt(3)) sin pi/48 cos pi/48 cos pi/24 cos pi/12 cos pi/6` = 3
Express the following as a sum or difference
sin 35° cos 28°
Express the following as a product
sin 50° + sin 40°
Express the following as a product
cos 35° – cos 75°
Show that `(sin 8x cos x - sin 6x cos 3x)/(cos 2x cos x - sin 3x sin 4x)` = tan 2x
Prove that `sin theta/2 sin (7theta)/2 + sin (3theta)/2 sin (11theta)/2` = sin 2θ sin 5θ
Prove that cos(30° – A) cos(30° + A) + cos(45° – A) cos(45° + A) = `cos 2"A" + 1/4`
If A + B + C = 180°, prove that `tan "A"/2 tan "B"/2 + tan "B"/2 tan "C"/2 + tan "C"/2 tan "A"/2` = 1
If A + B + C = `pi/2`, prove the following sin 2A + sin 2B + sin 2C = 4 cos A cos B cos C
Choose the correct alternative:
If `pi < 2theta < (3pi)/2`, then `sqrt(2 + sqrt(2 + 2cos4theta)` equals to
