ISC (Commerce)
ISC (Arts)
ISC (Science)
Academic Year: 2024-2025
Date: April 2025
Advertisements
- You are allowed an additional 15 minutes for only reading the paper.
- You must NOT start writing during reading time.
- The question paper has 12 printed pages.
- The Question Paper is divided into three sections and has 22 questions in all.
- Section A is compulsory and has fourteen questions.
- You are required to attempt all questions either from Section B or Section C.
- Section B and Section C have four questions each.
- Internal choices have been provided in two questions of 2 marks, two questions of 4 marks and two questions of 6 marks in Section A.
- Internal choices have been provided in one question of 2 marks and one question of 4 marks each in Section B and Section C.
- While attempting Multiple Choice Questions in Section A, B and C, you are required to write only ONE option as the answer.
- The intended marks for questions or parts of questions are given in the brackets [ ].
- All workings, including rough work, should be done on the same page as, and adjacent to, the rest of the answer.
- Mathematical tables and graph papers are provided.
A matrix which is both symmetric and skew symmetric matrix is a ______.
triangular matrix
identity matrix
diagonal matrix
null matrix
Chapter: [0.021] Matrices and Determinants
The value of `inta^x.e^x dx` equals
`(a^x.log_ea)e^x + c`
`(a^x.e^x)/(log_e(ae)) + c`
`(a^x.e^x)/(log_(ae)e) + c`
`log_e(ae)(ae)^x + c`
Chapter: [0.033] Integrals
The trigonometric equation tan–1x = 3tan–1 a has solution for ______.
`|a| ≤ 1/sqrt(3)`
`|a| > 1/sqrt(3)`
`|a| < 1/sqrt(3)`
all real value of a.
Chapter: [0.01] Relations and Functions (Section A)
Assertion: Degree of the differential equation: `a(dy/dx)^2 + bdx/dy = c`, is 3
Reason: If each term involving derivatives of a differential equation is a polynomial (or can be expressed as polynomial) then highest exponent of the highest order derivative is called the degree of the differential equation.
Which of the following is correct?
Both Assertion and Reason are true and Reason is the correct explanation for Assertion.
Both Assertion and Reason are true but Reason is not the correct explanation for Assertion.
Assertion is true and Reason is false.
Assertion is false and Reason is true.
Chapter: [0.034] Differential Equations
Five numbers x1, x2, x3, x4, x5 are randomly selected from the numbers 1, 2, 3, ......., 18 and are arranged in the increasing order such that x1 < x2 < x3 < x4 < x5. What is the probability that x2 = 7 and x4 = 11?
`26/51`
`3/104`
`1/68`
`1/34`
Chapter: [0.04] Probability (Section A)
if `|(a, b, c),(m, n, p),(x, y, z)| = k`, then what is the value of `|(6a, 2b, 2c),(3m, n, p),(3x, y, z)|`?
`k/6`
2k
3k
6k
Chapter: [0.021] Matrices and Determinants
Consider the graph `y = x^(1/3)`
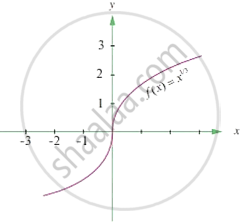
Statement 1: The above graph is continuous at x = 0
Statement 2: The above graph is differentiable at x = 0
Which of the following is correct?
Statement 1 is true and Statement 2 is false.
Statement 2 is true and Statement 1 is false.
Both the statements are true.
Both the statements are false.
Chapter: [0.031] Continuity, Differentiability and Differentiation
The value of `dy/dx` if y = |x – 1| + |x – 4| at x = 3 is ______.
–2
0
2
4
Chapter: [0.034] Differential Equations
Statement 1: The intersection of two equivalence relations is always an equivalence relation.
Statement 2: The Union of two equivalence relations is always an equivalence relation.
Which one of the following is correct?
Statement 1 implies Statement 2.
Statement 2 implies Statement 1.
Statement 1 is true only if Statement 2 is true.
Statement 1 and 2 are independent of each other.
Chapter: [0.01] Relations and Functions (Section A)
In a third order matrix aij denotes the element of the ith row and the jth column.
A = `a_(ij) = {(0",", for, i = j),(1",", f or, i > j),(-1",", f or, i < j):}`
Assertion: Matrix ‘A’ is not invertible.
Reason: Determinant A = 0
Which of the following is correct?
Both Assertion and Reason are true and Reason is the correct explanation for Assertion.
Both Assertion and Reason are true but Reason is not the correct explanation for Assertion.
Assertion is true and Reason is false.
Assertion is false and Reason is true.
Chapter: [0.021] Matrices and Determinants
Given two events A and B such that (A/B) = 0.25 and P(A ∩ B) = 0.12. The value P(A ∩ B') is ______.
0.36
0.48
0.88
0.036
Chapter: [0.04] Probability (Section A)
The value of the determinant of a matrix A of order 3 is 3. If C is the matrix of cofactors of the matrix A, then what is the value of determinant of C2?
Chapter: [0.021] Matrices and Determinants
If a relation R on the set {a, b, c} defined by R = {(b, b)}, then classify the relation.
Chapter: [0.01] Relations and Functions (Section A)

The given function f : R → R is not ‘onto’ function. Give reason.
Chapter: [0.01] Relations and Functions (Section A)
There are three machines and 2 of them are faulty. They are tested one by one in a random order till both the faulty machines are identified. What is the probability that only two tests are needed to identify the faulty machines?
Chapter: [0.04] Probability (Section A)
If xy = yx, then find `dy/dx`
Chapter: [0.031] Continuity, Differentiability and Differentiation
Find the interval in which the function f(x) = x2e–x is strictly increasing or decreasing.
Chapter: [0.032] Applications of Derivatives
Evaluate:
`int_0^sqrt(2)[x^2]dx`
Chapter: [0.033] Integrals
Find the equation to the tangent at (0, 0) on the curve y = 4x2 – 2x3
Chapter: [0.032] Applications of Derivatives
Evaluate:
`int(2x^3 - 1)/(x^4 + x)dx`
Chapter: [0.033] Integrals
Evaluate:
`inte^x "cosec" x(1 - cot x)dx`
Chapter: [0.033] Integrals
Advertisements
Find the value of `tan^-1(x/y) + tan^-1((y - x)/(y + x))`
Chapter: [0.01] Relations and Functions (Section A)
Solve:
sin–1(x) + sin–1(1 – x) = cos–1x.
Chapter: [0.01] Relations and Functions (Section A)
Evaluate:
`intsqrt(sec x/2 - 1)dx`
Chapter: [0.033] Integrals
A kite is being pulled down by a string that goes through a ring on the ground 8 meters away from the person pulling it. If the string is pulled in at 1 meter per second, how fast is the kite coming down when it is 15 meters high?
Chapter: [0.032] Applications of Derivatives
If `y = (x + sqrt(a^2 + x^2))^m`, prove that `(a^2 + x^2)(d^2y)/(dx^2) + xdy/dx - m^2y = 0`
Chapter: [0.031] Continuity, Differentiability and Differentiation
Three friends go to a restaurant to have pizza. They decide who will pay for the pizza by tossing a coin. It is decided that each one of them will toss a coin and if one person gets a different result (heads or tails) than the other two, that person would pay. If all three get the same result (all heads or all tails), they will toss again until they get a different result.
- What is the probability that all three friends will get the same result (all heads or all tails) in one round of tossing?
- What is the probability that they will get a different result in one round of tossing?
- What is the probability that they will need exactly four rounds of tossing to determine who would pay?
Chapter: [0.04] Probability (Section A)
Students of under graduation submitted a case study on “Understanding the Probability of Left-Handedness in Children Based on Parental Handedness”. Following Recent studies suggest that roughly 12% of the world population is left-handed. Depending on the parents’ handedness, the chances of having a left-handed child are as follows:
Scenario A: Both parents are left-handed, with a 24% chance of the child being left-handed.
Scenario B: The fathers is right-handed and the mothers left-handed, with a 22% chance of child being left-handed.
Scenario C: The fathers left-handed and the mother is right-handed, with a 17% chance of child being left-handed.
Scenario D: Both parents are right-handed, with a 9% chance of having a left-handed child.
Assuming that scenarios A, B, C and D are equally likely and L denotes the event that the child is left-handed, answer the following questions.
- What is the overall probability that a randomly selected child is left-handed?
- Given that exactly one parent is left-handed, what is the probability that a randomly selected child is left-handed?
- If a child is left-handed, what is the probability that both parents are left-handed?
Chapter: [0.04] Probability (Section A)
| To raise money for an orphanage, students of three schools A, B and C organised an exhibition in their residential colony, where they sold paper bags, scrap books and pastel sheets made by using recycled paper. Student of school A sold 30 paper bags, 20 scrap books and 10 pastel sheets and raised ₹ 410. Student of school B sold 20 paper bags, 10 scrap books and 20 pastel sheets and raised ₹ 290. Student of school C sold 20 paper bags, 20 scrap books and 20 pastel sheets and raised ₹ 440. |
Answer the following question:
- Translate the problem into a system of equations.
- Solve the system of equation by using matrix method.
- Hence, find the cost of one paper bag, one scrap book and one pastel sheet.
Chapter: [0.021] Matrices and Determinants
Solve the differential equation:
`(xdy - ydx) ysin(y/x) = (ydx + xdy) xcos(y/x)`.
Find the particular solution satisfying the condition that y = π when x = 1.
Chapter: [0.034] Differential Equations
Evaluate:
`int_0^π(sin^4x + cos^4x)dx`
Chapter: [0.033] Integrals
Hence evaluate:
`int_(-2π)^(2π) (sin^4x + cos^4x)/(1 + e^x)dx`
Chapter: [0.033] Integrals
Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to \[ \frac{2}{3} \] of the diameter of the sphere.
Chapter: [0.032] Applications of Derivatives
A given quantity of metal is to be cast into a half cylinder with a rectangular base and semicircular ends. Show that in order that the total surface area may be minimum the ratio of the length of the cylinder to the diameter of its semi-circular ends is \[\pi : (\pi + 2)\].
Chapter: [0.032] Applications of Derivatives
Kiran plays a game of throwing a fair die 3 times but to quit as and when she gets a six. Kiran gets +1 point for a six and –1 for any other number.

- If X denotes the random variable “points earned” then what are the possible values X can take?
- Find the probability distribution of this random variable X.
- Find the expected value of the points she gets.
Chapter: [0.04] Probability (Section A)
Consider the following statements and choose the correct option:
Statement 1: If `veca` and `vecb` represents two adjacent sides of a parallelogram then the diagonals are represented by `veca + vecb` and `veca - vecb`.
Statement 2: If `veca` and `vecb` represents two diagonals of a parallelogram then the adjacent sides are represented by `2(veca + vecb)` and `2(veca - vecb)`.
Which of the following is correct?
Only Statement 1
Only Statement 2
Both Statements 1 and 2
Neither Statement 1 nor Statement 2
Chapter: [0.05] Vectors (Section B)
If a plane passes through the point (1, 1, 1) and is perpendicular to the line \[\frac{x - 1}{3} = \frac{y - 1}{0} = \frac{z - 1}{4}\] then its perpendicular distance from the origin is ______.
`3/4`
`4/3`
`7/5`
1
Chapter: [0.06] Three - Dimensional Geometry (Section B)
If the direction cosines of a line are `(1/c, 1/c, 1/c)` then ______.
0 < c < 1
c = ± 3
c > 2
c > 0
c = `±sqrt(3)`
Chapter: [0.05] Vectors (Section B)
If `veca` is a unit vector perpendicular to `vecb` and `(veca + 2vecb).(3veca - vecb) = -5`, find `|vecb|`.
Chapter: [0.05] Vectors (Section B)
Shown below is a cuboid. Find `vec(BA).vec(BC)`
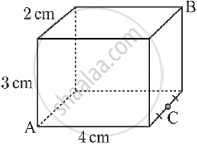
Chapter: [0.05] Vectors (Section B)
Advertisements
Find a vector of magnitude 9 units and perpendicular to the vectors.
`veca = 4hati - hatj + hatk` and `vecb = -2hati + hatj - 2hatk`
Chapter: [0.05] Vectors (Section B)
What are the values of x for which the angle between the vectors? `2x^2hati + 3xhatj + hatk` and `hati - 2hatj + x^2hatk` is obtuse?
Chapter: [0.05] Vectors (Section B)
Show that the line whose vector equation is `vecr = (2hati - 2hatj + 3hatk) + λ(hati - hatj + 4hatk)` is parallel to the plane whose vector equation is `vecr.(hati + 5hatj + hatk) = 5`. Also find the distance between them.
Chapter: [0.06] Three - Dimensional Geometry (Section B)
Find the equation of the plane containing the line `x/(-2) = (y - 1)/3 = (1 - z)/1` and the point (–1, 0, 2).
Chapter: [0.06] Three - Dimensional Geometry (Section B)
Sketch the region enclosed bounded by the curve, y = x |x| and the ordinates x = −1 and x = 1.
Chapter: [0.07] Application of Integrals (Section B)
Evaluate:
`int_0^1x^2dx`
Chapter: [0.07] Application of Integrals (Section B)
Hence find the area bounded by the curve, y = x |x| and the coordinates x = −1 and x = 1.
Chapter: [0.07] Application of Integrals (Section B)
Which condition is true if Average Cost (AC) is constant at all levels of output?
MC > AC
MC = AC
MC < AC
MC = `1/2` AC
Chapter: [0.08] Application of Calculus (Section C)
Read the following statements and choose the correct option:
- If r = 0, then regression lines are not defined.
- If r = 0, then regression lines are parallel.
- If r = 0, then regression lines are perpendicular.
- If r = ±1, then regression lines coincide.
Which of the following is correct?
Only IV is correct.
Only I and II are correct.
Only I and IV are correct.
Only III and IV are correct.
Chapter: [0.09] Linear Regression (Section C)
Mean of x = 53, mean of y = 28 regression co-efficient y on x = −1.2, regression co-efficient x on y = −0.3. Find coefficient of correlation (r).
Chapter: [0.09] Linear Regression (Section C)
The total revenue received from the sale of x unit of a product is given by R(x) = 3x2 + 36x + 5. Find the marginal revenue when x = 5.
Chapter: [0.08] Application of Calculus (Section C)
A manufacturing company finds that the daily cost of producing x item of product is given by C(x) = 210x + 7000. Find the minimum number that must be produced and sold daily, if each item is sold for ₹ 280.
Chapter: [0.08] Application of Calculus (Section C)
The cost function of a commodity is `C(x) = 200 + 20x - 1/2x^2` (in rupees). Find the range where AC falls.
Chapter: [0.08] Application of Calculus (Section C)
The demand function of a monopoly is given by x = 100 − 4p. Find the quantity at which the MR will be zero.
Chapter: [0.08] Application of Calculus (Section C)
A survey of 50 families to study the relationships between expenditure on accommodation in (₹ x) and expenditure on food and entertainment (₹ y) gave the following results: `sumx = 8500, sumy = 9600, σ_x = 60, σ_y = 20, r = 0.6`
Estimate the expenditure on food and entertainment when expenditure on accommodation is ₹ 200.
Chapter: [0.09] Linear Regression (Section C)
The random variables have regression lines 3x + 2y − 26 = 0 and 6x + y − 31 = 0. Calculate mean value of x and y.
Chapter: [0.09] Linear Regression (Section C)
The random variables have regression lines 3x + 2y − 26 = 0 and 6x + y − 31 = 0. Calculate co-efficient of correlations.
Chapter: [0.09] Linear Regression (Section C)
A linear programming problem is given by Z = px + qy where p, q > 0 subject to the constraints: x + y ≤ 60, 5x + y ≤ 100, x ≥ 0 and y ≥ 0
- Solve graphically to find the corner points of the feasible region.
- If Z = px + qy is maximum at (0, 60) and (10, 50), find the relation of p and q. Also mention the number of optimal solution(s) in this case.
Chapter: [0.1] Linear Programming (Section C)
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CISCE previous year question papers Class 12 Mathematics with solutions 2024 - 2025
Previous year Question paper for CISCE Class 12 -2025 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CISCE Class 12.
How CISCE Class 12 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
