Advertisements
Advertisements
प्रश्न
Form the differential equation of all parabolas whose axis is the X-axis.
उत्तर
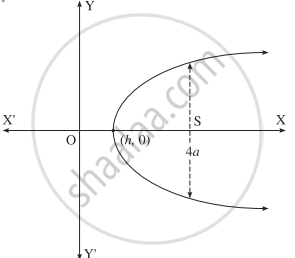
The equation of the parbola whose axis is the X-axis is y2 = 4a(x - h), ....(1)
where a and h are arbitrary constants.
Differentiating (1) w.r.t. x, we get
`"2y"("dy"/"dx") = 4"a"(1 - 0)`
∴ y`"dy"/"dx" = "2a"`
Differentiating again w.r.t. x, we get
`"y" * "d"/"dx"("dy"/"dx") + "dy"/"dx" * "dy"/"dx" = 0`
∴ `"y"("d"^2"y")/"dx"^2 + ("dy"/"dx")^2 = 0`
This is the required D.E.
APPEARS IN
संबंधित प्रश्न
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
(y - a)2 = 4(x - b)
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
y = c1e2x + c2e5x
Find the differential equation of the ellipse whose major axis is twice its minor axis.
In the following example verify that the given expression is a solution of the corresponding differential equation:
y = `(sin^-1 "x")^2 + "c"; (1 - "x"^2) ("d"^2"y")/"dx"^2 - "x" "dy"/"dx" = 2`
Solve the following differential equation:
`"y" - "x" "dy"/"dx" = 0`
Solve the following differential equation:
`"dy"/"dx" = - "k",` where k is a constant.
Solve the following differential equation:
`(cos^2y)/x dy + (cos^2x)/y dx` = 0
For the following differential equation find the particular solution satisfying the given condition:
3ex tan y dx + (1 + ex) sec2 y dy = 0, when x = 0, y = π.
Reduce the following differential equation to the variable separable form and hence solve:
`("x - y")^2 "dy"/"dx" = "a"^2`
Reduce the following differential equation to the variable separable form and hence solve:
(2x - 2y + 3)dx - (x - y + 1)dy = 0, when x = 0, y = 1.
Choose the correct option from the given alternatives:
x2 + y2 = a2 is a solution of
Choose the correct option from the given alternatives:
The solution of `("x + y")^2 "dy"/"dx" = 1` is
The integrating factor of linear differential equation `x dy/dx + 2y = x^2 log x` is ______.
In the following example verify that the given function is a solution of the differential equation.
`"y" = "e"^"ax" sin "bx"; ("d"^2"y")/"dx"^2 - 2"a" "dy"/"dx" + ("a"^2 + "b"^2)"y" = 0`
In the following example verify that the given function is a solution of the differential equation.
`"xy" = "ae"^"x" + "be"^-"x" + "x"^2; "x" ("d"^2"y")/"dx"^2 + 2 "dy"/"dx" + "x"^2 = "xy" + 2`
In the following example verify that the given function is a solution of the differential equation.
`"x"^2 = "2y"^2 log "y", "x"^2 + "y"^2 = "xy" "dx"/"dy"`
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
(y - a)2 = b(x + 4)
Obtain the differential equation by eliminating the arbitrary constants from the following equation:
y = `"Ae"^(3"x" + 1) + "Be"^(- 3"x" + 1)`
Form the differential equation of all the lines which are normal to the line 3x + 2y + 7 = 0.
Form the differential equation of the hyperbola whose length of transverse and conjugate axes are half of that of the given hyperbola `"x"^2/16 - "y"^2/36 = "k"`.
Solve the following differential equation:
`"dy"/"dx" = ("2y" - "x")/("2y + x")`
Solve the following differential equation:
y log y = (log y2 - x) `"dy"/"dx"`
Find the particular solution of the following differential equation:
`"dy"/"dx" - 3"y" cot "x" = sin "2x"`, when `"y"(pi/2) = 2`
Select and write the correct alternative from the given option for the question
General solution of `y - x ("d"y)/("d"x)` = 0 is
Form the differential equation of y = (c1 + c2)ex
Verify y = log x + c is the solution of differential equation `x ("d"^2y)/("d"x^2) + ("d"y)/("d"x)` = 0
Find the differential equation of the family of circles passing through the origin and having their centres on the x-axis
Find the differential equation of the curve represented by xy = aex + be–x + x2
If `x^2 y^2 = sin^-1 sqrt(x^2 + y^2) + cos^-1 sqrt(x^2 + y^2)`, then `"dy"/"dx"` = ?
The differential equation of all lines perpendicular to the line 5x + 2y + 7 = 0 is ____________.
If m and n are respectively the order and degree of the differential equation of the family of parabolas with focus at the origin and X-axis as its axis, then mn - m + n = ______.
The differential equation of all parabolas whose axis is Y-axis, is ______.
The differential equation of the family of circles touching Y-axis at the origin is ______.
Form the differential equation whose general solution is y = a cos 2x + b sin 2x.
A particle is moving along the X-axis. Its acceleration at time t is proportional to its velocity at that time. Find the differential equation of the motion of the particle.
