Advertisements
Advertisements
Question
\[\cos^2 x\frac{dy}{dx} + y = \tan x\]
Solution
We have,
\[ \cos^2 x\frac{dy}{dx} + y = \tan x\]
\[ \Rightarrow \frac{dy}{dx} + \left( \sec^2 x \right)y = \left( \tan x \right) \sec^2 x\]
\[\text{Comparing with }\frac{dy}{dx} + Px = Q,\text{ we get}\]
\[P = \sec^2 x \]
\[Q = \left( \tan x \right)\left( \sec^2 x \right)\]
Now,
\[I . F . = e^{\int \sec^2 x dx} = e^{\tan x} \]
So, the solution is given by
\[y \times e^{\tan x} = \int\left( \tan x \right)\left( \sec^2 x \right) \times e^{\tan x} dx + C\]
\[ \Rightarrow y e^{\tan x} = I + C . . . . . . . . . . \left( 1 \right)\]
Now,
\[I = \int\left( \tan x \right)\left( \sec^2 x \right) \times e^{\tan x} dx\]
Putting `t = tan x,` we get
\[dt = \sec^2 x dx\]
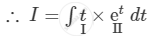
\[ = t \times \int e^t dt - \int\left( \frac{d t}{d t} \times \int e^t dt \right)dt\]
\[ = t e^t - \int e^t dt\]
\[ = t e^t - e^t \]
\[ \Rightarrow I = \tan x e^{\tan x} - e^{\tan x} = e^{\tan x} \left( \tan x - 1 \right)\]
Putting the value of `I` in (1), we get
\[y e^{\tan x} = e^{\tan x} \left( \tan x - 1 \right) + C\]
APPEARS IN
RELATED QUESTIONS
If `y=sqrt(sinx+sqrt(sinx+sqrt(sinx+..... oo))),` then show that `dy/dx=cosx/(2y-1)`
Find the differential equation representing the curve y = cx + c2.
Find the general solution of the following differential equation :
`(1+y^2)+(x-e^(tan^(-1)y))dy/dx= 0`
Find `(dy)/(dx)` at x = 1, y = `pi/4` if `sin^2 y + cos xy = K`
if `y = sin^(-1) (6xsqrt(1-9x^2))`, `1/(3sqrt2) < x < 1/(3sqrt2)` then find `(dy)/(dx)`
Write the order of the differential equation associated with the primitive y = C1 + C2 ex + C3 e−2x + C4, where C1, C2, C3, C4 are arbitrary constants.
The solution of the differential equation \[\frac{dy}{dx} = 1 + x + y^2 + x y^2 , y\left( 0 \right) = 0\] is
If m and n are the order and degree of the differential equation \[\left( y_2 \right)^5 + \frac{4 \left( y_2 \right)^3}{y_3} + y_3 = x^2 - 1\], then
The solution of the differential equation (x2 + 1) \[\frac{dy}{dx}\] + (y2 + 1) = 0, is
The number of arbitrary constants in the particular solution of a differential equation of third order is
Write the solution of the differential equation \[\frac{dy}{dx} = 2^{- y}\] .
Solve the differential equation (x2 − yx2) dy + (y2 + x2y2) dx = 0, given that y = 1, when x = 1.
cos (x + y) dy = dx
\[\frac{dy}{dx} - y \tan x = e^x \sec x\]
(x2 + 1) dy + (2y − 1) dx = 0
\[\frac{dy}{dx} + 2y = \sin 3x\]
\[\left( 1 + y^2 \right) + \left( x - e^{- \tan^{- 1} y} \right)\frac{dy}{dx} = 0\]
Solve the differential equation:
(1 + y2) dx = (tan−1 y − x) dy
`(dy)/(dx)+ y tan x = x^n cos x, n ne− 1`
Solve the following differential equation:- `y dx + x log (y)/(x)dy-2x dy=0`
Find a particular solution of the following differential equation:- x2 dy + (xy + y2) dx = 0; y = 1 when x = 1
The general solution of the differential equation `"dy"/"dx" = "e"^(x - y)` is ______.
The general solution of the differential equation `"dy"/"dx" + y/x` = 1 is ______.
y = x is a particular solution of the differential equation `("d"^2y)/("d"x^2) - x^2 "dy"/"dx" + xy` = x.
Find the general solution of (1 + tany)(dx – dy) + 2xdy = 0.
If y = e–x (Acosx + Bsinx), then y is a solution of ______.
Solution of differential equation xdy – ydx = 0 represents : ______.
Solution of `("d"y)/("d"x) - y` = 1, y(0) = 1 is given by ______.
The solution of `("d"y)/("d"x) + y = "e"^-x`, y(0) = 0 is ______.
Integrating factor of the differential equation `("d"y)/("d"x) + y tanx - secx` = 0 is ______.
y = aemx+ be–mx satisfies which of the following differential equation?
The general solution of `("d"y)/("d"x) = 2x"e"^(x^2 - y)` is ______.
The differential equation for which y = acosx + bsinx is a solution, is ______.
The general solution of the differential equation (ex + 1) ydy = (y + 1) exdx is ______.
The solution of the differential equation ydx + (x + xy)dy = 0 is ______.
Which of the following differential equations has `y = x` as one of its particular solution?
Find the general solution of the differential equation:
`(dy)/(dx) = (3e^(2x) + 3e^(4x))/(e^x + e^-x)`
