Advertisements
Advertisements
Question
If `sqrt(3) tan θ` = 1, then find the value of sin2θ – cos2θ.
Solution
Given that,
`sqrt(3) tan θ` = 1
⇒ tan θ = `1/sqrt(3)` = tan 30°
⇒ θ = 30°
Now, sin2θ – cos2θ = sin230° – cos230°
= `(1/2)^2 - (sqrt(3)/2)^2`
= `1/4 - 3/4`
= `(1 - 3)/4`
= `-2/4`
= `-1/2`
APPEARS IN
RELATED QUESTIONS
Prove the following trigonometric identities.
`sqrt((1 - cos theta)/(1 + cos theta)) = cosec theta - cot theta`
Prove the following trigonometric identities.
`(cos^2 theta)/sin theta - cosec theta + sin theta = 0`
Prove the following trigonometric identities.
`1/(sec A + tan A) - 1/cos A = 1/cos A - 1/(sec A - tan A)`
If sin θ + cos θ = x, prove that `sin^6 theta + cos^6 theta = (4- 3(x^2 - 1)^2)/4`
Prove the following identities:
`(sinAtanA)/(1 - cosA) = 1 + secA`
`1+(tan^2 theta)/((1+ sec theta))= sec theta`
`1+((tan^2 theta) cot theta)/(cosec^2 theta) = tan theta`
`(cot ^theta)/((cosec theta+1)) + ((cosec theta + 1))/cot theta = 2 sec theta`
If `sec theta = x ,"write the value of tan" theta`.
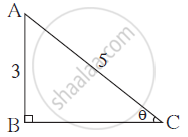
From the figure find the value of sinθ.
If sec θ + tan θ = x, write the value of sec θ − tan θ in terms of x.
If \[\sin \theta = \frac{4}{5}\] what is the value of cotθ + cosecθ?
Prove the following identity :
`(cosecA)/(cosecA - 1) + (cosecA)/(cosecA + 1) = 2sec^2A`
Without using trigonometric table , evaluate :
`sin72^circ/cos18^circ - sec32^circ/(cosec58^circ)`
Evaluate:
sin2 34° + sin2 56° + 2 tan 18° tan 72° – cot2 30°
If tan θ = 2, where θ is an acute angle, find the value of cos θ.
Prove that :
2(sin6 θ + cos6 θ) − 3 (sin4 θ + cos4 θ) + 1 = 0
Prove that tan2Φ + cot2Φ + 2 = sec2Φ.cosec2Φ.
Prove that `(cot "A" + "cosec A" - 1)/(cot "A" - "cosec A" + 1) = (1 + cos "A")/sin "A"`
Prove that sin6A + cos6A = 1 – 3sin2A . cos2A
