Advertisements
Advertisements
Question
Solve the following initial value problem:-
Solution
We have,
Clearly, it is a linear differential equation of the form
Integrating both sides with respect to x, we get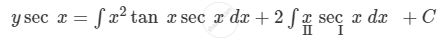
Now,
APPEARS IN
RELATED QUESTIONS
If 1,
Assume that a rain drop evaporates at a rate proportional to its surface area. Form a differential equation involving the rate of change of the radius of the rain drop.
Verify that y =
Show that y = ex (A cos x + B sin x) is the solution of the differential equation
Differential equation
Function y = log x
(1 − x2) dy + xy dx = xy2 dx
Solve the following differential equation:
Solve the differential equation
Find the particular solution of the differential equation
In a bank principal increases at the rate of 5% per year. An amount of Rs 1000 is deposited with this bank, how much will it worth after 10 years (e0.5 = 1.648).
Solve the following initial value problem:-
Solve the following initial value problem:
The rate of growth of a population is proportional to the number present. If the population of a city doubled in the past 25 years, and the present population is 100000, when will the city have a population of 500000?
If the interest is compounded continuously at 6% per annum, how much worth Rs 1000 will be after 10 years? How long will it take to double Rs 1000?
Find the equation of the curve passing through the point
Find the equation of the curve which passes through the point (1, 2) and the distance between the foot of the ordinate of the point of contact and the point of intersection of the tangent with x-axis is twice the abscissa of the point of contact.
The normal to a given curve at each point (x, y) on the curve passes through the point (3, 0). If the curve contains the point (3, 4), find its equation.
The rate of increase of bacteria in a culture is proportional to the number of bacteria present and it is found that the number doubles in 6 hours. Prove that the bacteria becomes 8 times at the end of 18 hours.
Verify that the function y = e−3x is a solution of the differential equation
Form the differential equation representing the family of curves y = a sin (x + b), where a, b are arbitrary constant.
If a + ib =
In each of the following examples, verify that the given function is a solution of the corresponding differential equation.
| Solution | D.E. |
| y = ex |
The solution of
State whether the following is True or False:
The integrating factor of the differential equation
Solve the differential equation
For the differential equation, find the particular solution
Verify y =
y =
Consider
=
=
Hence y =
Solve the following differential equation
Solution:
Put
∴
∴
∴ (1) becomes
∴
∴
Integrating, we get
∴
∴
∴
∴
Integrating factor of the differential equation
The differential equation (1 + y2)x dx – (1 + x2)y dy = 0 represents a family of:
