Question

Solve the following initial value problem:-

\[\frac{dy}{dx} + y \tan x = 2x + x^2 \tan x, y\left( 0 \right) = 1\]

Answer 1

We have,
\[\frac{dy}{dx} + y \tan x = 2x + x^2 \tan x . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dy}{dx} + Py = Q\]
\[\text{ where }P = \tan x\text{ and }Q = x^2 \cot x + 2x\]
\[ \therefore I . F . = e^{\int P\ dx} \]
\[ = e^{\int\tan x dx} \]
\[ = e^{log\left| \sec x \right|} = \sec x\]
\[\text{Multiplying both sides of }\left( 1 \right)\text{ by }I.F.= \sec x,\text{ we get }\]
\[\sec x\left( \frac{dy}{dx} + y\tan x \right) = \sec x\left( x^2 \tan x + 2x \right)\]
\[ \Rightarrow \sec x\left( \frac{dy}{dx} + y\tan x \right) = x^2 \tan x \sec x + 2x \sec x\]
Integrating both sides with respect to x, we get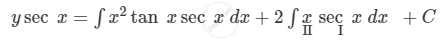

\[ \Rightarrow y \sec x = \int x^2 \tan x \sec x dx + 2sec x\int x dx - 2\int\left[ \frac{d}{dx}\left( sec x \right)\int x dx \right]dx + C\]
\[ \Rightarrow y \sec x = \int x^2 \tan x \sec\ x dx + x^2 \sec x - \int x^2 \tan x \sec x dx + C\]
\[ \Rightarrow y \sec x = x^2 \sec x + C\]
\[ \Rightarrow y = x^2 + C\cos x . . . . . \left( 2 \right)\]
Now, 
\[y\left( 0 \right) = 1\]
\[ \therefore 1 = 0 + C\cos 0\]
\[ \Rightarrow C = 1\]
\[\text{Putting the value of C in }\left( 2 \right),\text{ we get }\]
\[y = x^2 + \cos x\]
\[\text{ Hence, }y = x^2 + \cos x\text{ is the required solution .}\]