Advertisements
Advertisements
प्रश्न
The slope of the tangent at each point of a curve is equal to the sum of the coordinates of the point. Find the curve that passes through the origin.
उत्तर
According to the question,
\[\frac{dy}{dx} = x + y\]
\[\Rightarrow \frac{dy}{dx} - y = x\]
\[\text{ Comparing with }\frac{dy}{dx} + Py = Q,\text{ we get }\]
\[P = - 1\]
\[Q = x\]
Now,
\[I . F . = e^{- \int dx} = e^{- x} \]
So, the solution is given by
\[y \times I . F . = \int Q \times I . F . dx + C\]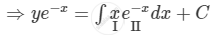
\[ \Rightarrow y e^{- x} = x\int e^{- x} dx - \int\left[ \frac{d}{dx}\left( x \right)\int e^{- x} dx \right]dx + C\]
\[ \Rightarrow y e^{- x} = - x e^{- x} + \int e^{- x} dx + C\]
\[ \Rightarrow y e^{- x} = - x e^{- x} - e^{- x} + C\]
Since the curve passes throught the origin, it satisfies the equation of the curve .
\[ \Rightarrow 0 e^0 = - 0 e^0 - e^0 + C\]
\[ \Rightarrow C = 1\]
Putting the value of C in the equation of the curve, we get
\[y e^{- x} = - x e^{- x} - e^{- x} + 1\]
\[ \Rightarrow y e^{- x} + x e^{- x} + e^{- x} = 1\]
\[ \Rightarrow \left( y + x + 1 \right) e^{- x} = 1\]
\[ \Rightarrow \left( x + y + 1 \right) = e^x \]
APPEARS IN
संबंधित प्रश्न
Prove that:
`int_0^(2a)f(x)dx = int_0^af(x)dx + int_0^af(2a - x)dx`
Show that the differential equation of which y = 2(x2 − 1) + \[c e^{- x^2}\] is a solution, is \[\frac{dy}{dx} + 2xy = 4 x^3\]
Show that the function y = A cos x + B sin x is a solution of the differential equation \[\frac{d^2 y}{d x^2} + y = 0\]
Show that y = ex (A cos x + B sin x) is the solution of the differential equation \[\frac{d^2 y}{d x^2} - 2\frac{dy}{dx} + 2y = 0\]
Differential equation \[\frac{d^2 y}{d x^2} - 2\frac{dy}{dx} + y = 0, y \left( 0 \right) = 1, y' \left( 0 \right) = 2\] Function y = xex + ex
C' (x) = 2 + 0.15 x ; C(0) = 100
y (1 + ex) dy = (y + 1) ex dx
(y2 + 1) dx − (x2 + 1) dy = 0
Solve the following differential equation:
\[xy\frac{dy}{dx} = 1 + x + y + xy\]
Find the particular solution of edy/dx = x + 1, given that y = 3, when x = 0.
x2 dy + y (x + y) dx = 0
(x2 − y2) dx − 2xy dy = 0
(x + 2y) dx − (2x − y) dy = 0
Solve the following initial value problem:-
\[x\frac{dy}{dx} - y = \left( x + 1 \right) e^{- x} , y\left( 1 \right) = 0\]
Solve the following initial value problem:-
\[\frac{dy}{dx} + y \tan x = 2x + x^2 \tan x, y\left( 0 \right) = 1\]
Solve the following initial value problem:
\[\frac{dy}{dx} + y \cot x = 4x\text{ cosec }x, y\left( \frac{\pi}{2} \right) = 0\]
The population of a city increases at a rate proportional to the number of inhabitants present at any time t. If the population of the city was 200000 in 1990 and 250000 in 2000, what will be the population in 2010?
Show that the equation of the curve whose slope at any point is equal to y + 2x and which passes through the origin is y + 2 (x + 1) = 2e2x.
The integrating factor of the differential equation (x log x)
\[\frac{dy}{dx} + y = 2 \log x\], is given by
The differential equation obtained on eliminating A and B from y = A cos ωt + B sin ωt, is
If xmyn = (x + y)m+n, prove that \[\frac{dy}{dx} = \frac{y}{x} .\]
y2 dx + (x2 − xy + y2) dy = 0
In the following verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:-
y = ex + 1 y'' − y' = 0
Find the equation of the plane passing through the point (1, -2, 1) and perpendicular to the line joining the points A(3, 2, 1) and B(1, 4, 2).
In the following example, verify that the given function is a solution of the corresponding differential equation.
| Solution | D.E. |
| y = xn | `x^2(d^2y)/dx^2 - n xx (xdy)/dx + ny =0` |
Solve the following differential equation.
(x2 − y2 ) dx + 2xy dy = 0
Solve the differential equation:
`e^(dy/dx) = x`
The differential equation (1 + y2)x dx – (1 + x2)y dy = 0 represents a family of:
