Question

The slope of the tangent at each point of a curve is equal to the sum of the coordinates of the point. Find the curve that passes through the origin.

Answer 1

According to the question,
\[\frac{dy}{dx} = x + y\]
\[\Rightarrow \frac{dy}{dx} - y = x\]
\[\text{ Comparing with }\frac{dy}{dx} + Py = Q,\text{ we get }\]
\[P = - 1\]
\[Q = x\]
Now, 
\[I . F . = e^{- \int dx} = e^{- x} \]
So, the solution is given by
\[y \times I . F . = \int Q \times I . F . dx + C\]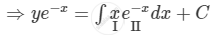

\[ \Rightarrow y e^{- x} = x\int e^{- x} dx - \int\left[ \frac{d}{dx}\left( x \right)\int e^{- x} dx \right]dx + C\]
\[ \Rightarrow y e^{- x} = - x e^{- x} + \int e^{- x} dx + C\]
\[ \Rightarrow y e^{- x} = - x e^{- x} - e^{- x} + C\]
Since the curve passes throught the origin, it satisfies the equation of the curve . 
\[ \Rightarrow 0 e^0 = - 0 e^0 - e^0 + C\]
\[ \Rightarrow C = 1\]
Putting the value of C in the equation of the curve, we get
\[y e^{- x} = - x e^{- x} - e^{- x} + 1\]
\[ \Rightarrow y e^{- x} + x e^{- x} + e^{- x} = 1\]
\[ \Rightarrow \left( y + x + 1 \right) e^{- x} = 1\]
\[ \Rightarrow \left( x + y + 1 \right) = e^x \]