Question

Solve the following initial value problem:-
\[x\frac{dy}{dx} - y = \log x, y\left( 1 \right) = 0\]

Answer 1

We have, 
\[x\frac{dy}{dx} - y = \log x\]
\[ \Rightarrow \frac{dy}{dx} - \frac{y}{x} = \frac{\log x}{x} . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dy}{dx} + Py = Q\]
\[\text{ where }P = - \frac{1}{x}\text{ and }Q = \frac{\log x}{x}\]
\[ \therefore I.F. = e^{\int P\ dx} \]
\[ = e^{- \int\frac{1}{x} dx} \]
\[ = e^{- \log x} \]
\[ = \frac{1}{x}\]
\[\text{ Multiplying both sides of }\left( 1 \right)\text{ by }I . F . = \frac{1}{x}, \text{ we get }\]
\[\frac{1}{x} \left( \frac{dy}{dx} - \frac{1}{x}y \right) = \frac{1}{x} \times \frac{\log x}{x}\]
\[ \Rightarrow \frac{1}{x}\frac{dy}{dx} - \frac{1}{x^2}y = \frac{\log x}{x^2}\]
Integrating both sides with respect to x, we get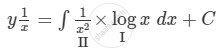

\[ \Rightarrow \frac{y}{x} = \log x\int\frac{1}{x^2}dx - \int\left[ \frac{d}{dx}\left( \log x \right)\int\frac{1}{x^2}dx \right]dx + C\]
\[ \Rightarrow \frac{y}{x} = - \frac{\log x}{x} + \int\frac{1}{x^2}dx + C\]
\[ \Rightarrow \frac{y}{x} = - \frac{\log x}{x} - \frac{1}{x} + C\]
\[ \Rightarrow y = - \log x - 1 + Cx . . . . . . . . . \left( 2 \right)\]
Now,
\[y\left( 1 \right) = 0\]
\[ \therefore 0 = - 0 - 1 + C\left( 1 \right)\]
\[ \Rightarrow C = 1\]
\[\text{ Putting the value of C in }\left( 2 \right),\text{ we get }\]
\[y = - \log x - 1 + x\]
\[ \Rightarrow y = x - 1 - \log x\]
\[\text{ Hence, }y = x - 1 - \log x\text{ is the required solution .}\]