Advertisements
Advertisements
प्रश्न
Solve the following initial value problem:-
\[x\frac{dy}{dx} - y = \log x, y\left( 1 \right) = 0\]
उत्तर
We have,
\[x\frac{dy}{dx} - y = \log x\]
\[ \Rightarrow \frac{dy}{dx} - \frac{y}{x} = \frac{\log x}{x} . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dy}{dx} + Py = Q\]
\[\text{ where }P = - \frac{1}{x}\text{ and }Q = \frac{\log x}{x}\]
\[ \therefore I.F. = e^{\int P\ dx} \]
\[ = e^{- \int\frac{1}{x} dx} \]
\[ = e^{- \log x} \]
\[ = \frac{1}{x}\]
\[\text{ Multiplying both sides of }\left( 1 \right)\text{ by }I . F . = \frac{1}{x}, \text{ we get }\]
\[\frac{1}{x} \left( \frac{dy}{dx} - \frac{1}{x}y \right) = \frac{1}{x} \times \frac{\log x}{x}\]
\[ \Rightarrow \frac{1}{x}\frac{dy}{dx} - \frac{1}{x^2}y = \frac{\log x}{x^2}\]
Integrating both sides with respect to x, we get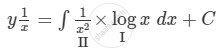
\[ \Rightarrow \frac{y}{x} = \log x\int\frac{1}{x^2}dx - \int\left[ \frac{d}{dx}\left( \log x \right)\int\frac{1}{x^2}dx \right]dx + C\]
\[ \Rightarrow \frac{y}{x} = - \frac{\log x}{x} + \int\frac{1}{x^2}dx + C\]
\[ \Rightarrow \frac{y}{x} = - \frac{\log x}{x} - \frac{1}{x} + C\]
\[ \Rightarrow y = - \log x - 1 + Cx . . . . . . . . . \left( 2 \right)\]
Now,
\[y\left( 1 \right) = 0\]
\[ \therefore 0 = - 0 - 1 + C\left( 1 \right)\]
\[ \Rightarrow C = 1\]
\[\text{ Putting the value of C in }\left( 2 \right),\text{ we get }\]
\[y = - \log x - 1 + x\]
\[ \Rightarrow y = x - 1 - \log x\]
\[\text{ Hence, }y = x - 1 - \log x\text{ is the required solution .}\]
APPEARS IN
संबंधित प्रश्न
Assume that a rain drop evaporates at a rate proportional to its surface area. Form a differential equation involving the rate of change of the radius of the rain drop.
Form the differential equation of the family of hyperbolas having foci on x-axis and centre at the origin.
Show that Ax2 + By2 = 1 is a solution of the differential equation x \[\left\{ y\frac{d^2 y}{d x^2} + \left( \frac{dy}{dx} \right)^2 \right\} = y\frac{dy}{dx}\]
Verify that y = − x − 1 is a solution of the differential equation (y − x) dy − (y2 − x2) dx = 0.
Show that y = e−x + ax + b is solution of the differential equation\[e^x \frac{d^2 y}{d x^2} = 1\]
Solve the differential equation \[x\frac{dy}{dx} + \cot y = 0\] given that \[y = \frac{\pi}{4}\], when \[x=\sqrt{2}\]
Solve the differential equation \[\frac{dy}{dx} = \frac{2x\left( \log x + 1 \right)}{\sin y + y \cos y}\], given that y = 0, when x = 1.
In a culture the bacteria count is 100000. The number is increased by 10% in 2 hours. In how many hours will the count reach 200000, if the rate of growth of bacteria is proportional to the number present.
x2 dy + y (x + y) dx = 0
Solve the following initial value problem:-
\[\frac{dy}{dx} + 2y = e^{- 2x} \sin x, y\left( 0 \right) = 0\]
Solve the following initial value problem:
\[\frac{dy}{dx} + y \cot x = 4x\text{ cosec }x, y\left( \frac{\pi}{2} \right) = 0\]
Solve the following initial value problem:-
\[\frac{dy}{dx} + 2y \tan x = \sin x; y = 0\text{ when }x = \frac{\pi}{3}\]
Solve the following initial value problem:-
\[dy = \cos x\left( 2 - y\text{ cosec }x \right)dx\]
The surface area of a balloon being inflated, changes at a rate proportional to time t. If initially its radius is 1 unit and after 3 seconds it is 2 units, find the radius after time t.
A population grows at the rate of 5% per year. How long does it take for the population to double?
If the marginal cost of manufacturing a certain item is given by C' (x) = \[\frac{dC}{dx}\] = 2 + 0.15 x. Find the total cost function C (x), given that C (0) = 100.
Find the equation of the curve passing through the point \[\left( 1, \frac{\pi}{4} \right)\] and tangent at any point of which makes an angle tan−1 \[\left( \frac{y}{x} - \cos^2 \frac{y}{x} \right)\] with x-axis.
The slope of the tangent at each point of a curve is equal to the sum of the coordinates of the point. Find the curve that passes through the origin.
Find the solution of the differential equation
\[x\sqrt{1 + y^2}dx + y\sqrt{1 + x^2}dy = 0\]
The differential equation obtained on eliminating A and B from y = A cos ωt + B sin ωt, is
Verify that the function y = e−3x is a solution of the differential equation \[\frac{d^2 y}{d x^2} + \frac{dy}{dx} - 6y = 0.\]
Form the differential equation of the family of circles having centre on y-axis and radius 3 unit.
The price of six different commodities for years 2009 and year 2011 are as follows:
| Commodities | A | B | C | D | E | F |
|
Price in 2009 (₹) |
35 | 80 | 25 | 30 | 80 | x |
| Price in 2011 (₹) | 50 | y | 45 | 70 | 120 | 105 |
The Index number for the year 2011 taking 2009 as the base year for the above data was calculated to be 125. Find the values of x andy if the total price in 2009 is ₹ 360.
Choose the correct option from the given alternatives:
The solution of `1/"x" * "dy"/"dx" = tan^-1 "x"` is
In the following example, verify that the given function is a solution of the corresponding differential equation.
| Solution | D.E. |
| xy = log y + k | y' (1 - xy) = y2 |
Determine the order and degree of the following differential equations.
| Solution | D.E. |
| ax2 + by2 = 5 | `xy(d^2y)/dx^2+ x(dy/dx)^2 = y dy/dx` |
Form the differential equation from the relation x2 + 4y2 = 4b2
Solve the following differential equation.
x2y dx − (x3 + y3 ) dy = 0
Solve the following differential equation.
`(x + y) dy/dx = 1`
`xy dy/dx = x^2 + 2y^2`
Verify y = `a + b/x` is solution of `x(d^2y)/(dx^2) + 2 (dy)/(dx)` = 0
y = `a + b/x`
`(dy)/(dx) = square`
`(d^2y)/(dx^2) = square`
Consider `x(d^2y)/(dx^2) + 2(dy)/(dx)`
= `x square + 2 square`
= `square`
Hence y = `a + b/x` is solution of `square`
Given that `"dy"/"dx" = "e"^-2x` and y = 0 when x = 5. Find the value of x when y = 3.
