Question

The tangent at any point (x, y) of a curve makes an angle tan⁻¹(2x + 3y) with x-axis. Find the equation of the curve if it passes through (1, 2).

Answer 1

The slope of the curve is given as \[\frac{dy}{dx} = \tan \theta\] Here,
\[\theta = \tan^{- 1} \left( 2x + 3y \right)\]
\[ \therefore \frac{dy}{dx} = \tan\left( \tan^{- 1} 2x + 3y \right)\]
\[ \Rightarrow \frac{dy}{dx} = 2x + 3y\]
\[\Rightarrow \frac{dy}{dx} - 3y = 2x . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dy}{dx} + Py = Q\]
\[\text{ where }P = - 3\text{ and }Q = 2x\]
\[ \therefore I . F . = e^{\int P\ dx} \]
\[ = e^{\int - 3 dx} \]
\[ = e^{- 3x} \]
\[\text{ Multiplying both sides of }(1),\text{ by }I . F . = e^{- 3x} , \text{ we get }\]
\[ e^{- 3x} \left( \frac{dy}{dx} - 3y \right) = e^{- 3x} . 2x\]
\[ \Rightarrow e^{- 3x} \left( \frac{dy}{dx} - 3y \right) = 2x e^{- 3x} \]
Integrating both sides with respect to x, we get
\[y e^{- 3x} = 2\int x e^{- 3x} dx + C\]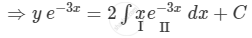

\[ \Rightarrow y e^{- 3x} = 2x\int e^{- 3x} dx - 2\int\left[ \frac{d}{dx}\left( x \right)\int e^{- 3x} dx \right]dx + C\]
\[ \Rightarrow y e^{- 3x} = - 2x\frac{e^{- 3x}}{3} + 2 \times \frac{1}{3}\int e^{- 3x} dx + C\]
\[ \Rightarrow y e^{- 3x} = - \frac{2}{3}x e^{- 3x} - 2 \times \frac{1}{9} e^{- 3x} + C\]
\[ \Rightarrow y e^{- 3x} = - \frac{2}{3}x e^{- 3x} - \frac{2}{9} e^{- 3x} + C\]
\[\text{ Since the curve passes through }\left( 1, 2 \right),\text{ it satisfies the above equation.}\]
\[ \therefore 2 e^{- 3} = - \frac{2}{3} e^{- 3} - \frac{2}{9} e^{- 3} + C\]
\[ \Rightarrow C = 2 e^{- 3} + \frac{2}{3} e^{- 3} + \frac{2}{9} e^{- 3} \]
\[ \Rightarrow C = \frac{26}{9} e^{- 3} \]
Putting the value of C, we get
\[y e^{- 3x} = \left( - \frac{2}{3}x - \frac{2}{9} \right) e^{- 3x} + \frac{26}{9} e^{- 3} \]