Advertisements
Advertisements
प्रश्न
Find the equation of the curve such that the portion of the x-axis cut off between the origin and the tangent at a point is twice the abscissa and which passes through the point (1, 2).
उत्तर
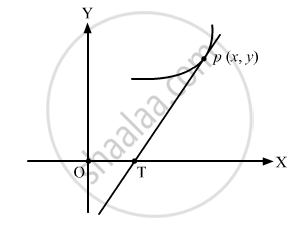
Portion of the x-axis cut off between the origin and tangent at a point \[= x - y \hspace{0.167em} \hspace{0.167em} \frac{dx}{dy} = OT\]
It is given, OT = 2x
\[\begin{array}{l}\therefore \hspace{0.167em} \hspace{0.167em} x - y \hspace{0.167em} \hspace{0.167em} \frac{dx}{dy} = 2x \\ - x = y\frac{dx}{dy} \\ - \int\frac{dx}{x} = \int\frac{dy}{y} \\ \therefore \hspace{0.167em} \hspace{0.167em} xy = k\end{array}\]
Since the curve passes through the point (1, 2)
⇒ at x = 1 ⇒ y = 2
∴ k = 2
∴ xy = 2
APPEARS IN
संबंधित प्रश्न
Prove that:
`int_0^(2a)f(x)dx = int_0^af(x)dx + int_0^af(2a - x)dx`
Show that the differential equation of which y = 2(x2 − 1) + \[c e^{- x^2}\] is a solution, is \[\frac{dy}{dx} + 2xy = 4 x^3\]
Show that the function y = A cos x + B sin x is a solution of the differential equation \[\frac{d^2 y}{d x^2} + y = 0\]
Hence, the given function is the solution to the given differential equation. \[\frac{c - x}{1 + cx}\] is a solution of the differential equation \[(1+x^2)\frac{dy}{dx}+(1+y^2)=0\].
For the following differential equation verify that the accompanying function is a solution:
| Differential equation | Function |
|
\[x^3 \frac{d^2 y}{d x^2} = 1\]
|
\[y = ax + b + \frac{1}{2x}\]
|
Differential equation \[\frac{d^2 y}{d x^2} + y = 0, y \left( 0 \right) = 0, y' \left( 0 \right) = 1\] Function y = sin x
C' (x) = 2 + 0.15 x ; C(0) = 100
Solve the following differential equation:
\[y\left( 1 - x^2 \right)\frac{dy}{dx} = x\left( 1 + y^2 \right)\]
Solve the differential equation \[\frac{dy}{dx} = \frac{2x\left( \log x + 1 \right)}{\sin y + y \cos y}\], given that y = 0, when x = 1.
3x2 dy = (3xy + y2) dx
The population of a city increases at a rate proportional to the number of inhabitants present at any time t. If the population of the city was 200000 in 1990 and 250000 in 2000, what will be the population in 2010?
Find the equation of the curve passing through the point \[\left( 1, \frac{\pi}{4} \right)\] and tangent at any point of which makes an angle tan−1 \[\left( \frac{y}{x} - \cos^2 \frac{y}{x} \right)\] with x-axis.
The tangent at any point (x, y) of a curve makes an angle tan−1(2x + 3y) with x-axis. Find the equation of the curve if it passes through (1, 2).
At every point on a curve the slope is the sum of the abscissa and the product of the ordinate and the abscissa, and the curve passes through (0, 1). Find the equation of the curve.
Radium decomposes at a rate proportional to the quantity of radium present. It is found that in 25 years, approximately 1.1% of a certain quantity of radium has decomposed. Determine approximately how long it will take for one-half of the original amount of radium to decompose?
The slope of the tangent at each point of a curve is equal to the sum of the coordinates of the point. Find the curve that passes through the origin.
The integrating factor of the differential equation (x log x)
\[\frac{dy}{dx} + y = 2 \log x\], is given by
The price of six different commodities for years 2009 and year 2011 are as follows:
| Commodities | A | B | C | D | E | F |
|
Price in 2009 (₹) |
35 | 80 | 25 | 30 | 80 | x |
| Price in 2011 (₹) | 50 | y | 45 | 70 | 120 | 105 |
The Index number for the year 2011 taking 2009 as the base year for the above data was calculated to be 125. Find the values of x andy if the total price in 2009 is ₹ 360.
Choose the correct alternative.
The solution of `x dy/dx = y` log y is
Solve:
(x + y) dy = a2 dx
x2y dx – (x3 + y3) dy = 0
Solve the following differential equation `("d"y)/("d"x)` = x2y + y
Solve: `("d"y)/("d"x) + 2/xy` = x2
Solve the following differential equation
`yx ("d"y)/("d"x)` = x2 + 2y2
Integrating factor of the differential equation `"dy"/"dx" - y` = cos x is ex.
Solution of `x("d"y)/("d"x) = y + x tan y/x` is `sin(y/x)` = cx
The value of `dy/dx` if y = |x – 1| + |x – 4| at x = 3 is ______.
