Advertisements
Advertisements
Question
Find the equation of the curve such that the portion of the x-axis cut off between the origin and the tangent at a point is twice the abscissa and which passes through the point (1, 2).
Solution
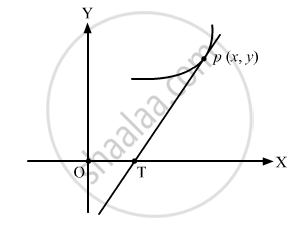
Portion of the x-axis cut off between the origin and tangent at a point \[= x - y \hspace{0.167em} \hspace{0.167em} \frac{dx}{dy} = OT\]
It is given, OT = 2x
\[\begin{array}{l}\therefore \hspace{0.167em} \hspace{0.167em} x - y \hspace{0.167em} \hspace{0.167em} \frac{dx}{dy} = 2x \\ - x = y\frac{dx}{dy} \\ - \int\frac{dx}{x} = \int\frac{dy}{y} \\ \therefore \hspace{0.167em} \hspace{0.167em} xy = k\end{array}\]
Since the curve passes through the point (1, 2)
⇒ at x = 1 ⇒ y = 2
∴ k = 2
∴ xy = 2
APPEARS IN
RELATED QUESTIONS
If 1, `omega` and `omega^2` are the cube roots of unity, prove `(a + b omega + c omega^2)/(c + s omega + b omega^2) = omega^2`
Verify that y2 = 4ax is a solution of the differential equation y = x \[\frac{dy}{dx} + a\frac{dx}{dy}\]
For the following differential equation verify that the accompanying function is a solution:
| Differential equation | Function |
|
\[x + y\frac{dy}{dx} = 0\]
|
\[y = \pm \sqrt{a^2 - x^2}\]
|
For the following differential equation verify that the accompanying function is a solution:
| Differential equation | Function |
|
\[x^3 \frac{d^2 y}{d x^2} = 1\]
|
\[y = ax + b + \frac{1}{2x}\]
|
Differential equation \[\frac{d^2 y}{d x^2} - y = 0, y \left( 0 \right) = 2, y' \left( 0 \right) = 0\] Function y = ex + e−x
Solve the differential equation \[x\frac{dy}{dx} + \cot y = 0\] given that \[y = \frac{\pi}{4}\], when \[x=\sqrt{2}\]
The volume of a spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of the balloon after `t` seconds.
In a bank principal increases at the rate of r% per year. Find the value of r if ₹100 double itself in 10 years (loge 2 = 0.6931).
(x + 2y) dx − (2x − y) dy = 0
In a simple circuit of resistance R, self inductance L and voltage E, the current `i` at any time `t` is given by L \[\frac{di}{dt}\]+ R i = E. If E is constant and initially no current passes through the circuit, prove that \[i = \frac{E}{R}\left\{ 1 - e^{- \left( R/L \right)t} \right\}.\]
The normal to a given curve at each point (x, y) on the curve passes through the point (3, 0). If the curve contains the point (3, 4), find its equation.
The slope of the tangent at each point of a curve is equal to the sum of the coordinates of the point. Find the curve that passes through the origin.
The x-intercept of the tangent line to a curve is equal to the ordinate of the point of contact. Find the particular curve through the point (1, 1).
The solution of the differential equation \[\frac{dy}{dx} - \frac{y\left( x + 1 \right)}{x} = 0\] is given by
Which of the following transformations reduce the differential equation \[\frac{dz}{dx} + \frac{z}{x}\log z = \frac{z}{x^2} \left( \log z \right)^2\] into the form \[\frac{du}{dx} + P\left( x \right) u = Q\left( x \right)\]
What is integrating factor of \[\frac{dy}{dx}\] + y sec x = tan x?
The integrating factor of the differential equation \[x\frac{dy}{dx} - y = 2 x^2\]
If xmyn = (x + y)m+n, prove that \[\frac{dy}{dx} = \frac{y}{x} .\]
If a + ib = `("x" + "iy")/("x" - "iy"),` prove that `"a"^2 +"b"^2 = 1` and `"b"/"a" = (2"xy")/("x"^2 - "y"^2)`
The price of six different commodities for years 2009 and year 2011 are as follows:
| Commodities | A | B | C | D | E | F |
|
Price in 2009 (₹) |
35 | 80 | 25 | 30 | 80 | x |
| Price in 2011 (₹) | 50 | y | 45 | 70 | 120 | 105 |
The Index number for the year 2011 taking 2009 as the base year for the above data was calculated to be 125. Find the values of x andy if the total price in 2009 is ₹ 360.
For each of the following differential equations find the particular solution.
(x − y2 x) dx − (y + x2 y) dy = 0, when x = 2, y = 0
Solve the following differential equation.
xdx + 2y dx = 0
Solve the following differential equation.
y dx + (x - y2 ) dy = 0
x2y dx – (x3 + y3) dy = 0
y dx – x dy + log x dx = 0
For the differential equation, find the particular solution (x – y2x) dx – (y + x2y) dy = 0 when x = 2, y = 0
For the differential equation, find the particular solution
`("d"y)/("d"x)` = (4x +y + 1), when y = 1, x = 0
Choose the correct alternative:
Differential equation of the function c + 4yx = 0 is
The function y = ex is solution ______ of differential equation
The function y = cx is the solution of differential equation `("d"y)/("d"x) = y/x`
Find the particular solution of the following differential equation
`("d"y)/("d"x)` = e2y cos x, when x = `pi/6`, y = 0.
Solution: The given D.E. is `("d"y)/("d"x)` = e2y cos x
∴ `1/"e"^(2y) "d"y` = cos x dx
Integrating, we get
`int square "d"y` = cos x dx
∴ `("e"^(-2y))/(-2)` = sin x + c1
∴ e–2y = – 2sin x – 2c1
∴ `square` = c, where c = – 2c1
This is general solution.
When x = `pi/6`, y = 0, we have
`"e"^0 + 2sin pi/6` = c
∴ c = `square`
∴ particular solution is `square`
