Advertisements
Advertisements
Question
Solution
We have,
\[\frac{dy}{dx} = \log x\]
\[ \Rightarrow dy = \left( \log x \right)dx\]
Integrating both sides, we get
\[\int dy = \int\left( \log x \right)dx\]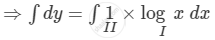
\[ \Rightarrow \int dy = \log x\int1 dx - \int\left[ \frac{d}{dx}\left( \log x \right)\int1 dx \right]dx\]
\[ \Rightarrow y = x\log x - \int\frac{x}{x}dx\]
\[ \Rightarrow y = x\log x - \int1dx\]
\[ \Rightarrow y = x\log x - x\]
\[ \Rightarrow y = x\left( \log x - 1 \right) + C\]
\[ \Rightarrow y = x\left( \log x - 1 \right) + C\]
\[\text{ So, } y = x\left( \log x - 1 \right) +\text{ C is defined for all }x \in R\text{ except }x = 0.\]
\[\text{ Hence, } y = x\left( \log x - 1 \right) +\text{ C, where } x \in R - \left\{ 0 \right\},\text{ is the solution to the given differential equation.}\]
APPEARS IN
RELATED QUESTIONS
If 1, `omega` and `omega^2` are the cube roots of unity, prove `(a + b omega + c omega^2)/(c + s omega + b omega^2) = omega^2`
Verify that y = 4 sin 3x is a solution of the differential equation \[\frac{d^2 y}{d x^2} + 9y = 0\]
Verify that y = \[\frac{a}{x} + b\] is a solution of the differential equation
\[\frac{d^2 y}{d x^2} + \frac{2}{x}\left( \frac{dy}{dx} \right) = 0\]
Show that y = ax3 + bx2 + c is a solution of the differential equation \[\frac{d^3 y}{d x^3} = 6a\].
Hence, the given function is the solution to the given differential equation. \[\frac{c - x}{1 + cx}\] is a solution of the differential equation \[(1+x^2)\frac{dy}{dx}+(1+y^2)=0\].
Show that y = ex (A cos x + B sin x) is the solution of the differential equation \[\frac{d^2 y}{d x^2} - 2\frac{dy}{dx} + 2y = 0\]
For the following differential equation verify that the accompanying function is a solution:
| Differential equation | Function |
|
\[x + y\frac{dy}{dx} = 0\]
|
\[y = \pm \sqrt{a^2 - x^2}\]
|
For the following differential equation verify that the accompanying function is a solution:
| Differential equation | Function |
|
\[x\frac{dy}{dx} + y = y^2\]
|
\[y = \frac{a}{x + a}\]
|
(1 − x2) dy + xy dx = xy2 dx
y (1 + ex) dy = (y + 1) ex dx
y ex/y dx = (xex/y + y) dy
Find the equation of the curve which passes through the point (1, 2) and the distance between the foot of the ordinate of the point of contact and the point of intersection of the tangent with x-axis is twice the abscissa of the point of contact.
The slope of a curve at each of its points is equal to the square of the abscissa of the point. Find the particular curve through the point (−1, 1).
Find the equation of the curve that passes through the point (0, a) and is such that at any point (x, y) on it, the product of its slope and the ordinate is equal to the abscissa.
Which of the following transformations reduce the differential equation \[\frac{dz}{dx} + \frac{z}{x}\log z = \frac{z}{x^2} \left( \log z \right)^2\] into the form \[\frac{du}{dx} + P\left( x \right) u = Q\left( x \right)\]
Show that y = ae2x + be−x is a solution of the differential equation \[\frac{d^2 y}{d x^2} - \frac{dy}{dx} - 2y = 0\]
y2 dx + (x2 − xy + y2) dy = 0
Verify that the function y = e−3x is a solution of the differential equation \[\frac{d^2 y}{d x^2} + \frac{dy}{dx} - 6y = 0.\]
Form the differential equation of the family of circles having centre on y-axis and radius 3 unit.
Find the particular solution of the differential equation `"dy"/"dx" = "xy"/("x"^2+"y"^2),`given that y = 1 when x = 0
In the following example, verify that the given function is a solution of the corresponding differential equation.
| Solution | D.E. |
| y = xn | `x^2(d^2y)/dx^2 - n xx (xdy)/dx + ny =0` |
For the following differential equation find the particular solution.
`(x + 1) dy/dx − 1 = 2e^(−y)`,
when y = 0, x = 1
Solve the following differential equation.
y2 dx + (xy + x2 ) dy = 0
Solve the following differential equation.
`xy dy/dx = x^2 + 2y^2`
Solve the differential equation:
`e^(dy/dx) = x`
x2y dx – (x3 + y3) dy = 0
The function y = ex is solution ______ of differential equation
Solve the following differential equation
`y log y ("d"x)/("d"y) + x` = log y
Verify y = `a + b/x` is solution of `x(d^2y)/(dx^2) + 2 (dy)/(dx)` = 0
y = `a + b/x`
`(dy)/(dx) = square`
`(d^2y)/(dx^2) = square`
Consider `x(d^2y)/(dx^2) + 2(dy)/(dx)`
= `x square + 2 square`
= `square`
Hence y = `a + b/x` is solution of `square`
Given that `"dy"/"dx"` = yex and x = 0, y = e. Find the value of y when x = 1.
`d/(dx)(tan^-1 (sqrt(1 + x^2) - 1)/x)` is equal to:
