Advertisements
Advertisements
Question
Solution
We have,
\[\frac{dy}{dx} = \tan^{- 1} x\]
\[ \Rightarrow dy = \left( \tan^{- 1} x \right)dx\]
Integrating both sides, we get
\[\int dy = \int\left( \tan^{- 1} x \right)dx\]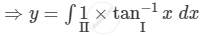
\[ \Rightarrow y = \tan^{- 1} x\int1 dx - \int\left[ \frac{d}{dx}\left( \tan^{- 1} x \right)\int1 dx \right]dx\]
\[ \Rightarrow y = x \tan^{- 1} x - \int\frac{x}{1 + x^2}dx\]
\[ \Rightarrow y = x \tan^{- 1} x - \frac{1}{2}\int\frac{2x}{1 + x^2}dx\]
\[ \Rightarrow y = x \tan^{- 1} x - \frac{1}{2}\log\left| 1 + x^2 \right| + C\]
\[\text{ So, } y = x \tan^{- 1} x - \frac{1}{2}\log\left| 1 + x^2 \right| +\text{C is defined for all }x \in R.\]
\[\text{ Hence, } y = x \tan^{- 1} x - \frac{1}{2}\log\left| 1 + x^2 \right| +\text{C is the solution to the given differential equation.}\]
APPEARS IN
RELATED QUESTIONS
For the following differential equation verify that the accompanying function is a solution:
| Differential equation | Function |
|
\[y = \left( \frac{dy}{dx} \right)^2\]
|
\[y = \frac{1}{4} \left( x \pm a \right)^2\]
|
Differential equation \[\frac{d^2 y}{d x^2} + y = 0, y \left( 0 \right) = 0, y' \left( 0 \right) = 1\] Function y = sin x
Differential equation \[\frac{d^2 y}{d x^2} - y = 0, y \left( 0 \right) = 2, y' \left( 0 \right) = 0\] Function y = ex + e−x
xy (y + 1) dy = (x2 + 1) dx
x cos2 y dx = y cos2 x dy
Solve the differential equation \[\frac{dy}{dx} = \frac{2x\left( \log x + 1 \right)}{\sin y + y \cos y}\], given that y = 0, when x = 1.
Find the particular solution of the differential equation \[\frac{dy}{dx} = - 4x y^2\] given that y = 1, when x = 0.
The volume of a spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of the balloon after `t` seconds.
Find the particular solution of the differential equation
(1 – y2) (1 + log x) dx + 2xy dy = 0, given that y = 0 when x = 1.
Solve the following initial value problem:-
\[dy = \cos x\left( 2 - y\text{ cosec }x \right)dx\]
The surface area of a balloon being inflated, changes at a rate proportional to time t. If initially its radius is 1 unit and after 3 seconds it is 2 units, find the radius after time t.
A bank pays interest by continuous compounding, that is, by treating the interest rate as the instantaneous rate of change of principal. Suppose in an account interest accrues at 8% per year, compounded continuously. Calculate the percentage increase in such an account over one year.
Experiments show that radium disintegrates at a rate proportional to the amount of radium present at the moment. Its half-life is 1590 years. What percentage will disappear in one year?
Find the curve for which the intercept cut-off by a tangent on x-axis is equal to four times the ordinate of the point of contact.
Find the equation of the curve that passes through the point (0, a) and is such that at any point (x, y) on it, the product of its slope and the ordinate is equal to the abscissa.
Write the differential equation obtained eliminating the arbitrary constant C in the equation xy = C2.
The differential equation \[x\frac{dy}{dx} - y = x^2\], has the general solution
Which of the following differential equations has y = C1 ex + C2 e−x as the general solution?
In the following verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:-
`y=sqrt(a^2-x^2)` `x+y(dy/dx)=0`
The price of six different commodities for years 2009 and year 2011 are as follows:
| Commodities | A | B | C | D | E | F |
|
Price in 2009 (₹) |
35 | 80 | 25 | 30 | 80 | x |
| Price in 2011 (₹) | 50 | y | 45 | 70 | 120 | 105 |
The Index number for the year 2011 taking 2009 as the base year for the above data was calculated to be 125. Find the values of x andy if the total price in 2009 is ₹ 360.
In each of the following examples, verify that the given function is a solution of the corresponding differential equation.
| Solution | D.E. |
| y = ex | `dy/ dx= y` |
Determine the order and degree of the following differential equations.
| Solution | D.E. |
| ax2 + by2 = 5 | `xy(d^2y)/dx^2+ x(dy/dx)^2 = y dy/dx` |
The differential equation of `y = k_1e^x+ k_2 e^-x` is ______.
Solve:
(x + y) dy = a2 dx
y2 dx + (xy + x2)dy = 0
Solve the following differential equation
`yx ("d"y)/("d"x)` = x2 + 2y2
Verify y = `a + b/x` is solution of `x(d^2y)/(dx^2) + 2 (dy)/(dx)` = 0
y = `a + b/x`
`(dy)/(dx) = square`
`(d^2y)/(dx^2) = square`
Consider `x(d^2y)/(dx^2) + 2(dy)/(dx)`
= `x square + 2 square`
= `square`
Hence y = `a + b/x` is solution of `square`
A man is moving away from a tower 41.6 m high at a rate of 2 m/s. If the eye level of the man is 1.6 m above the ground, then the rate at which the angle of elevation of the top of the tower changes, when he is at a distance of 30 m from the foot of the tower, is
