Question

x cos² y  dx = y cos² x dy

Answer 1

We have,
\[x \cos {}^2 y dx = y \cos {}^2 x dy\]
\[ \Rightarrow \frac{x}{\cos^2 x}dx = \frac{y}{\cos^2 y}dy\]
\[ \Rightarrow x \sec^2 x dx = y \sec^2 y dy\]
Integrating both sides, we get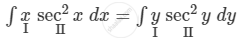 

\[ \Rightarrow x\int \sec^2 x dx - \int\left\{ \frac{d}{dx}\left( x \right)\int \sec^2 x dx \right\}dx = y\int \sec^2 y dy - \int\left\{ \frac{d}{dy}\left( y \right)\int \sec^2 y dy \right\}dy\]
\[ \Rightarrow x \tan x - \int\tan x dx = y \tan y - \int\tan y dy\]
\[ \Rightarrow x \tan x - \log \left| \sec x \right| = y \tan y - \log \left| \sec y \right| + C\]
\[ \Rightarrow x \tan x - y \tan y = \log \left| \sec x \right| - \log \left| \sec y \right| + C\]
\[\text{ Hence, }x \tan x - y \tan y = \log \left| \sec x \right| - \log \left| \sec y \right| +\text{C is the required solution.} \]