Question

\[\frac{1}{x}\frac{dy}{dx} = \tan^{- 1} x, x \neq 0\]

Answer 1

We have,
\[\frac{1}{x}\frac{dy}{dx} = \tan^{- 1} x\]
\[\Rightarrow \frac{dy}{dx} = x \tan^{- 1} x\]
\[ \Rightarrow dy = \left( x \tan^{- 1} x \right)dx\]
Integrating both sides, we get
\[\int dy = \int\left( x \tan^{- 1} x \right)dx\]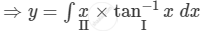

\[ \Rightarrow \int dy = \tan^{- 1} x\int x dx - \int\left[ \frac{d}{dx}\left( \tan^{- 1} x \right)\int x dx \right]dx\]
\[ \Rightarrow y = \frac{x^2 \tan^{- 1} x}{2} - \frac{1}{2}\int\frac{x^2}{1 + x^2}dx\]
\[ \Rightarrow y = \frac{x^2 \tan^{- 1} x}{2} - \frac{1}{2}\int\frac{x^2 + 1 - 1}{1 + x^2}dx\]
\[ \Rightarrow y = \frac{x^2 \tan^{- 1} x}{2} - \frac{1}{2}\int\left( 1 - \frac{1}{1 + x^2} \right)dx\]
\[ \Rightarrow y = \frac{x^2 \tan^{- 1} x}{2} - \frac{1}{2}x + \frac{\tan^{- 1} x}{2} + C\]
\[ \Rightarrow y = \frac{\left( x^2 + 1 \right) \tan^{- 1} x}{2} - \frac{1}{2}x + C\]
\[\text{ Hence, }y = \frac{\left( x^2 + 1 \right) \tan^{- 1} x}{2} - \frac{1}{2}x +\text{C is the solution to the given differential equation.}\]