Advertisements
Advertisements
प्रश्न
Advertisements
उत्तर
We have,
\[\frac{dy}{dx} = \log x\]
\[ \Rightarrow dy = \left( \log x \right)dx\]
Integrating both sides, we get
\[\int dy = \int\left( \log x \right)dx\]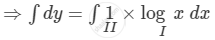
\[ \Rightarrow \int dy = \log x\int1 dx - \int\left[ \frac{d}{dx}\left( \log x \right)\int1 dx \right]dx\]
\[ \Rightarrow y = x\log x - \int\frac{x}{x}dx\]
\[ \Rightarrow y = x\log x - \int1dx\]
\[ \Rightarrow y = x\log x - x\]
\[ \Rightarrow y = x\left( \log x - 1 \right) + C\]
\[ \Rightarrow y = x\left( \log x - 1 \right) + C\]
\[\text{ So, } y = x\left( \log x - 1 \right) +\text{ C is defined for all }x \in R\text{ except }x = 0.\]
\[\text{ Hence, } y = x\left( \log x - 1 \right) +\text{ C, where } x \in R - \left\{ 0 \right\},\text{ is the solution to the given differential equation.}\]
APPEARS IN
संबंधित प्रश्न
Form the differential equation representing the family of ellipses having centre at the origin and foci on x-axis.
tan y \[\frac{dy}{dx}\] = sin (x + y) + sin (x − y)
Solve the following differential equation:
\[y\left( 1 - x^2 \right)\frac{dy}{dx} = x\left( 1 + y^2 \right)\]
(x + y) (dx − dy) = dx + dy
Solve the following initial value problem:-
\[y' + y = e^x , y\left( 0 \right) = \frac{1}{2}\]
Solve the following initial value problem:-
\[\frac{dy}{dx} + 2y = e^{- 2x} \sin x, y\left( 0 \right) = 0\]
Solve the following initial value problem:
\[x\frac{dy}{dx} + y = x \cos x + \sin x, y\left( \frac{\pi}{2} \right) = 1\]
Find the equation of the curve passing through the point \[\left( 1, \frac{\pi}{4} \right)\] and tangent at any point of which makes an angle tan−1 \[\left( \frac{y}{x} - \cos^2 \frac{y}{x} \right)\] with x-axis.
Find the curve for which the intercept cut-off by a tangent on x-axis is equal to four times the ordinate of the point of contact.
Find the equation of the curve which passes through the origin and has the slope x + 3y− 1 at any point (x, y) on it.
The equation of the curve whose slope is given by \[\frac{dy}{dx} = \frac{2y}{x}; x > 0, y > 0\] and which passes through the point (1, 1) is
If xmyn = (x + y)m+n, prove that \[\frac{dy}{dx} = \frac{y}{x} .\]
Form the differential equation representing the family of curves y = a sin (x + b), where a, b are arbitrary constant.
Form the differential equation of the family of circles having centre on y-axis and radius 3 unit.
If a + ib = `("x" + "iy")/("x" - "iy"),` prove that `"a"^2 +"b"^2 = 1` and `"b"/"a" = (2"xy")/("x"^2 - "y"^2)`
In the following example, verify that the given function is a solution of the corresponding differential equation.
| Solution | D.E. |
| y = xn | `x^2(d^2y)/dx^2 - n xx (xdy)/dx + ny =0` |
Determine the order and degree of the following differential equations.
| Solution | D.E |
| y = aex + be−x | `(d^2y)/dx^2= 1` |
Solve the following differential equation.
`dy/dx = x^2 y + y`
Solve the following differential equation.
`dy /dx +(x-2 y)/ (2x- y)= 0`
Solve the following differential equation.
`x^2 dy/dx = x^2 +xy - y^2`
Solve the following differential equation.
`(x + a) dy/dx = – y + a`
Solve the following differential equation y2dx + (xy + x2) dy = 0
A solution of differential equation which can be obtained from the general solution by giving particular values to the arbitrary constant is called ______ solution
Solve the differential equation `dy/dx + xy = xy^2` and find the particular solution when y = 4, x = 1.
Which of the following defines a differential equation?
Why is the equation \[x\frac{dy}{dx} + y = 0\] classified as a differential equation?
In mathematics and science, what primary purpose do differential equations serve?
