Advertisements
Advertisements
प्रश्न
Advertisements
उत्तर
We have,
\[\frac{dy}{dx} = \log x\]
\[ \Rightarrow dy = \left( \log x \right)dx\]
Integrating both sides, we get
\[\int dy = \int\left( \log x \right)dx\]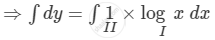
\[ \Rightarrow \int dy = \log x\int1 dx - \int\left[ \frac{d}{dx}\left( \log x \right)\int1 dx \right]dx\]
\[ \Rightarrow y = x\log x - \int\frac{x}{x}dx\]
\[ \Rightarrow y = x\log x - \int1dx\]
\[ \Rightarrow y = x\log x - x\]
\[ \Rightarrow y = x\left( \log x - 1 \right) + C\]
\[ \Rightarrow y = x\left( \log x - 1 \right) + C\]
\[\text{ So, } y = x\left( \log x - 1 \right) +\text{ C is defined for all }x \in R\text{ except }x = 0.\]
\[\text{ Hence, } y = x\left( \log x - 1 \right) +\text{ C, where } x \in R - \left\{ 0 \right\},\text{ is the solution to the given differential equation.}\]
APPEARS IN
संबंधित प्रश्न
Assume that a rain drop evaporates at a rate proportional to its surface area. Form a differential equation involving the rate of change of the radius of the rain drop.
Show that y = ax3 + bx2 + c is a solution of the differential equation \[\frac{d^3 y}{d x^3} = 6a\].
Verify that y = cx + 2c2 is a solution of the differential equation
For the following differential equation verify that the accompanying function is a solution:
| Differential equation | Function |
|
\[x + y\frac{dy}{dx} = 0\]
|
\[y = \pm \sqrt{a^2 - x^2}\]
|
Differential equation \[x\frac{dy}{dx} = 1, y\left( 1 \right) = 0\]
Function y = log x
Solve the following differential equation:
\[\text{ cosec }x \log y \frac{dy}{dx} + x^2 y^2 = 0\]
Find the particular solution of edy/dx = x + 1, given that y = 3, when x = 0.
Find the solution of the differential equation cos y dy + cos x sin y dx = 0 given that y = \[\frac{\pi}{2}\], when x = \[\frac{\pi}{2}\]
If y(x) is a solution of the different equation \[\left( \frac{2 + \sin x}{1 + y} \right)\frac{dy}{dx} = - \cos x\] and y(0) = 1, then find the value of y(π/2).
Solve the following initial value problem:-
\[\tan x\left( \frac{dy}{dx} \right) = 2x\tan x + x^2 - y; \tan x \neq 0\] given that y = 0 when \[x = \frac{\pi}{2}\]
A bank pays interest by continuous compounding, that is, by treating the interest rate as the instantaneous rate of change of principal. Suppose in an account interest accrues at 8% per year, compounded continuously. Calculate the percentage increase in such an account over one year.
The slope of the tangent at a point P (x, y) on a curve is \[\frac{- x}{y}\]. If the curve passes through the point (3, −4), find the equation of the curve.
The normal to a given curve at each point (x, y) on the curve passes through the point (3, 0). If the curve contains the point (3, 4), find its equation.
The integrating factor of the differential equation \[\left( 1 - y^2 \right)\frac{dx}{dy} + yx = ay\left( - 1 < y < 1 \right)\] is ______.
In the following verify that the given functions (explicit or implicit) is a solution of the corresponding differential equation:-
y = ex + 1 y'' − y' = 0
Find the differential equation whose general solution is
x3 + y3 = 35ax.
Solve the following differential equation.
(x2 − y2 ) dx + 2xy dy = 0
Solve the following differential equation.
`xy dy/dx = x^2 + 2y^2`
Solve the following differential equation.
`x^2 dy/dx = x^2 +xy - y^2`
Solve the following differential equation.
`dy/dx + y` = 3
The integrating factor of the differential equation `dy/dx - y = x` is e−x.
Solve the differential equation (x2 – yx2)dy + (y2 + xy2)dx = 0
Solve the following differential equation y2dx + (xy + x2) dy = 0
State whether the following statement is True or False:
The integrating factor of the differential equation `("d"y)/("d"x) - y` = x is e–x
Solve the following differential equation `("d"y)/("d"x)` = x2y + y
Solve the following differential equation `("d"y)/("d"x)` = cos(x + y)
Solution: `("d"y)/("d"x)` = cos(x + y) ......(1)
Put `square`
∴ `1 + ("d"y)/("d"x) = "dv"/("d"x)`
∴ `("d"y)/("d"x) = "dv"/("d"x) - 1`
∴ (1) becomes `"dv"/("d"x) - 1` = cos v
∴ `"dv"/("d"x)` = 1 + cos v
∴ `square` dv = dx
Integrating, we get
`int 1/(1 + cos "v") "d"v = int "d"x`
∴ `int 1/(2cos^2 ("v"/2)) "dv" = int "d"x`
∴ `1/2 int square "dv" = int "d"x`
∴ `1/2* (tan("v"/2))/(1/2)` = x + c
∴ `square` = x + c
An appropriate substitution to solve the differential equation `"dx"/"dy" = (x^2 log(x/y) - x^2)/(xy log(x/y))` is ______.
Integrating factor of the differential equation `"dy"/"dx" - y` = cos x is ex.
lf the straight lines `ax + by + p` = 0 and `x cos alpha + y sin alpha = p` are inclined at an angle π/4 and concurrent with the straight line `x sin alpha - y cos alpha` = 0, then the value of `a^2 + b^2` is
Solve the differential equation
`y (dy)/(dx) + x` = 0
