Advertisements
Advertisements
Question
The slope of the tangent at each point of a curve is equal to the sum of the coordinates of the point. Find the curve that passes through the origin.
Solution
According to the question,
\[\frac{dy}{dx} = x + y\]
\[\Rightarrow \frac{dy}{dx} - y = x\]
\[\text{ Comparing with }\frac{dy}{dx} + Py = Q,\text{ we get }\]
\[P = - 1\]
\[Q = x\]
Now,
\[I . F . = e^{- \int dx} = e^{- x} \]
So, the solution is given by
\[y \times I . F . = \int Q \times I . F . dx + C\]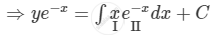
\[ \Rightarrow y e^{- x} = x\int e^{- x} dx - \int\left[ \frac{d}{dx}\left( x \right)\int e^{- x} dx \right]dx + C\]
\[ \Rightarrow y e^{- x} = - x e^{- x} + \int e^{- x} dx + C\]
\[ \Rightarrow y e^{- x} = - x e^{- x} - e^{- x} + C\]
Since the curve passes throught the origin, it satisfies the equation of the curve .
\[ \Rightarrow 0 e^0 = - 0 e^0 - e^0 + C\]
\[ \Rightarrow C = 1\]
Putting the value of C in the equation of the curve, we get
\[y e^{- x} = - x e^{- x} - e^{- x} + 1\]
\[ \Rightarrow y e^{- x} + x e^{- x} + e^{- x} = 1\]
\[ \Rightarrow \left( y + x + 1 \right) e^{- x} = 1\]
\[ \Rightarrow \left( x + y + 1 \right) = e^x \]
APPEARS IN
RELATED QUESTIONS
Assume that a rain drop evaporates at a rate proportional to its surface area. Form a differential equation involving the rate of change of the radius of the rain drop.
Verify that y = 4 sin 3x is a solution of the differential equation \[\frac{d^2 y}{d x^2} + 9y = 0\]
For the following differential equation verify that the accompanying function is a solution:
| Differential equation | Function |
|
\[x\frac{dy}{dx} = y\]
|
y = ax |
(sin x + cos x) dy + (cos x − sin x) dx = 0
Solve the following differential equation:
\[xy\frac{dy}{dx} = 1 + x + y + xy\]
Solve the following differential equation:
\[y\left( 1 - x^2 \right)\frac{dy}{dx} = x\left( 1 + y^2 \right)\]
In a bank principal increases at the rate of r% per year. Find the value of r if ₹100 double itself in 10 years (loge 2 = 0.6931).
If y(x) is a solution of the different equation \[\left( \frac{2 + \sin x}{1 + y} \right)\frac{dy}{dx} = - \cos x\] and y(0) = 1, then find the value of y(π/2).
Solve the following initial value problem:-
\[\left( 1 + y^2 \right) dx + \left( x - e^{- \tan^{- 1} y} \right) dx = 0, y\left( 0 \right) = 0\]
Solve the following initial value problem:
\[\frac{dy}{dx} + y \cot x = 4x\text{ cosec }x, y\left( \frac{\pi}{2} \right) = 0\]
Solve the following initial value problem:-
\[\frac{dy}{dx} + 2y \tan x = \sin x; y = 0\text{ when }x = \frac{\pi}{3}\]
If the interest is compounded continuously at 6% per annum, how much worth Rs 1000 will be after 10 years? How long will it take to double Rs 1000?
The population of a city increases at a rate proportional to the number of inhabitants present at any time t. If the population of the city was 200000 in 1990 and 250000 in 2000, what will be the population in 2010?
A bank pays interest by continuous compounding, that is, by treating the interest rate as the instantaneous rate of change of principal. Suppose in an account interest accrues at 8% per year, compounded continuously. Calculate the percentage increase in such an account over one year.
Experiments show that radium disintegrates at a rate proportional to the amount of radium present at the moment. Its half-life is 1590 years. What percentage will disappear in one year?
Find the equation of the curve passing through the point \[\left( 1, \frac{\pi}{4} \right)\] and tangent at any point of which makes an angle tan−1 \[\left( \frac{y}{x} - \cos^2 \frac{y}{x} \right)\] with x-axis.
Solve the following differential equation : \[y^2 dx + \left( x^2 - xy + y^2 \right)dy = 0\] .
Form the differential equation representing the family of curves y = a sin (x + b), where a, b are arbitrary constant.
The price of six different commodities for years 2009 and year 2011 are as follows:
| Commodities | A | B | C | D | E | F |
|
Price in 2009 (₹) |
35 | 80 | 25 | 30 | 80 | x |
| Price in 2011 (₹) | 50 | y | 45 | 70 | 120 | 105 |
The Index number for the year 2011 taking 2009 as the base year for the above data was calculated to be 125. Find the values of x andy if the total price in 2009 is ₹ 360.
Solve the following differential equation.
`y^3 - dy/dx = x dy/dx`
Solve the following differential equation.
`x^2 dy/dx = x^2 +xy - y^2`
Select and write the correct alternative from the given option for the question
Differential equation of the function c + 4yx = 0 is
Solve the differential equation sec2y tan x dy + sec2x tan y dx = 0
Solve the following differential equation
`yx ("d"y)/("d"x)` = x2 + 2y2
State whether the following statement is True or False:
The integrating factor of the differential equation `("d"y)/("d"x) - y` = x is e–x
Given that `"dy"/"dx"` = yex and x = 0, y = e. Find the value of y when x = 1.
Solve the differential equation `"dy"/"dx"` = 1 + x + y2 + xy2, when y = 0, x = 0.
The differential equation of all non horizontal lines in a plane is `("d"^2x)/("d"y^2)` = 0
