Advertisements
Advertisements
प्रश्न
Find the equation of the curve such that the portion of the x-axis cut off between the origin and the tangent at a point is twice the abscissa and which passes through the point (1, 2).
उत्तर
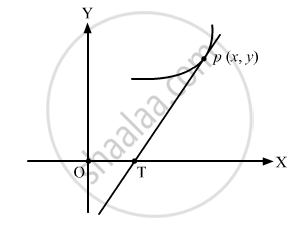
Portion of the x-axis cut off between the origin and tangent at a point \[= x - y \hspace{0.167em} \hspace{0.167em} \frac{dx}{dy} = OT\]
It is given, OT = 2x
\[\begin{array}{l}\therefore \hspace{0.167em} \hspace{0.167em} x - y \hspace{0.167em} \hspace{0.167em} \frac{dx}{dy} = 2x \\ - x = y\frac{dx}{dy} \\ - \int\frac{dx}{x} = \int\frac{dy}{y} \\ \therefore \hspace{0.167em} \hspace{0.167em} xy = k\end{array}\]
Since the curve passes through the point (1, 2)
⇒ at x = 1 ⇒ y = 2
∴ k = 2
∴ xy = 2
APPEARS IN
संबंधित प्रश्न
Solve the equation for x: `sin^(-1) 5/x + sin^(-1) 12/x = pi/2, x != 0`
Assume that a rain drop evaporates at a rate proportional to its surface area. Form a differential equation involving the rate of change of the radius of the rain drop.
Find the differential equation of all the parabolas with latus rectum '4a' and whose axes are parallel to x-axis.
For the following differential equation verify that the accompanying function is a solution:
| Differential equation | Function |
|
\[x^3 \frac{d^2 y}{d x^2} = 1\]
|
\[y = ax + b + \frac{1}{2x}\]
|
Differential equation \[\frac{dy}{dx} + y = 2, y \left( 0 \right) = 3\] Function y = e−x + 2
(1 + x2) dy = xy dx
Solve the differential equation \[\frac{dy}{dx} = \frac{2x\left( \log x + 1 \right)}{\sin y + y \cos y}\], given that y = 0, when x = 1.
x2 dy + y (x + y) dx = 0
y ex/y dx = (xex/y + y) dy
\[\frac{dy}{dx} = \frac{y}{x} + \sin\left( \frac{y}{x} \right)\]
If the interest is compounded continuously at 6% per annum, how much worth Rs 1000 will be after 10 years? How long will it take to double Rs 1000?
The slope of the tangent at a point P (x, y) on a curve is \[\frac{- x}{y}\]. If the curve passes through the point (3, −4), find the equation of the curve.
The rate of increase of bacteria in a culture is proportional to the number of bacteria present and it is found that the number doubles in 6 hours. Prove that the bacteria becomes 8 times at the end of 18 hours.
Write the differential equation obtained by eliminating the arbitrary constant C in the equation x2 − y2 = C2.
Solve the following differential equation : \[\left( \sqrt{1 + x^2 + y^2 + x^2 y^2} \right) dx + xy \ dy = 0\].
For each of the following differential equations find the particular solution.
(x − y2 x) dx − (y + x2 y) dy = 0, when x = 2, y = 0
For the following differential equation find the particular solution.
`(x + 1) dy/dx − 1 = 2e^(−y)`,
when y = 0, x = 1
Solve the following differential equation.
`xy dy/dx = x^2 + 2y^2`
The solution of `dy/ dx` = 1 is ______
Solve
`dy/dx + 2/ x y = x^2`
Solve the differential equation sec2y tan x dy + sec2x tan y dx = 0
Solve the following differential equation
`x^2 ("d"y)/("d"x)` = x2 + xy − y2
The function y = ex is solution ______ of differential equation
Solve the following differential equation `("d"y)/("d"x)` = cos(x + y)
Solution: `("d"y)/("d"x)` = cos(x + y) ......(1)
Put `square`
∴ `1 + ("d"y)/("d"x) = "dv"/("d"x)`
∴ `("d"y)/("d"x) = "dv"/("d"x) - 1`
∴ (1) becomes `"dv"/("d"x) - 1` = cos v
∴ `"dv"/("d"x)` = 1 + cos v
∴ `square` dv = dx
Integrating, we get
`int 1/(1 + cos "v") "d"v = int "d"x`
∴ `int 1/(2cos^2 ("v"/2)) "dv" = int "d"x`
∴ `1/2 int square "dv" = int "d"x`
∴ `1/2* (tan("v"/2))/(1/2)` = x + c
∴ `square` = x + c
Find the particular solution of the following differential equation
`("d"y)/("d"x)` = e2y cos x, when x = `pi/6`, y = 0.
Solution: The given D.E. is `("d"y)/("d"x)` = e2y cos x
∴ `1/"e"^(2y) "d"y` = cos x dx
Integrating, we get
`int square "d"y` = cos x dx
∴ `("e"^(-2y))/(-2)` = sin x + c1
∴ e–2y = – 2sin x – 2c1
∴ `square` = c, where c = – 2c1
This is general solution.
When x = `pi/6`, y = 0, we have
`"e"^0 + 2sin pi/6` = c
∴ c = `square`
∴ particular solution is `square`
Given that `"dy"/"dx"` = yex and x = 0, y = e. Find the value of y when x = 1.
Solve `x^2 "dy"/"dx" - xy = 1 + cos(y/x)`, x ≠ 0 and x = 1, y = `pi/2`
There are n students in a school. If r % among the students are 12 years or younger, which of the following expressions represents the number of students who are older than 12?
The value of `dy/dx` if y = |x – 1| + |x – 4| at x = 3 is ______.
