Advertisements
Advertisements
प्रश्न
The tangent at any point (x, y) of a curve makes an angle tan−1(2x + 3y) with x-axis. Find the equation of the curve if it passes through (1, 2).
उत्तर
The slope of the curve is given as \[\frac{dy}{dx} = \tan \theta\] Here,
\[\theta = \tan^{- 1} \left( 2x + 3y \right)\]
\[ \therefore \frac{dy}{dx} = \tan\left( \tan^{- 1} 2x + 3y \right)\]
\[ \Rightarrow \frac{dy}{dx} = 2x + 3y\]
\[\Rightarrow \frac{dy}{dx} - 3y = 2x . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dy}{dx} + Py = Q\]
\[\text{ where }P = - 3\text{ and }Q = 2x\]
\[ \therefore I . F . = e^{\int P\ dx} \]
\[ = e^{\int - 3 dx} \]
\[ = e^{- 3x} \]
\[\text{ Multiplying both sides of }(1),\text{ by }I . F . = e^{- 3x} , \text{ we get }\]
\[ e^{- 3x} \left( \frac{dy}{dx} - 3y \right) = e^{- 3x} . 2x\]
\[ \Rightarrow e^{- 3x} \left( \frac{dy}{dx} - 3y \right) = 2x e^{- 3x} \]
Integrating both sides with respect to x, we get
\[y e^{- 3x} = 2\int x e^{- 3x} dx + C\]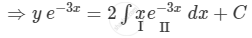
\[ \Rightarrow y e^{- 3x} = 2x\int e^{- 3x} dx - 2\int\left[ \frac{d}{dx}\left( x \right)\int e^{- 3x} dx \right]dx + C\]
\[ \Rightarrow y e^{- 3x} = - 2x\frac{e^{- 3x}}{3} + 2 \times \frac{1}{3}\int e^{- 3x} dx + C\]
\[ \Rightarrow y e^{- 3x} = - \frac{2}{3}x e^{- 3x} - 2 \times \frac{1}{9} e^{- 3x} + C\]
\[ \Rightarrow y e^{- 3x} = - \frac{2}{3}x e^{- 3x} - \frac{2}{9} e^{- 3x} + C\]
\[\text{ Since the curve passes through }\left( 1, 2 \right),\text{ it satisfies the above equation.}\]
\[ \therefore 2 e^{- 3} = - \frac{2}{3} e^{- 3} - \frac{2}{9} e^{- 3} + C\]
\[ \Rightarrow C = 2 e^{- 3} + \frac{2}{3} e^{- 3} + \frac{2}{9} e^{- 3} \]
\[ \Rightarrow C = \frac{26}{9} e^{- 3} \]
Putting the value of C, we get
\[y e^{- 3x} = \left( - \frac{2}{3}x - \frac{2}{9} \right) e^{- 3x} + \frac{26}{9} e^{- 3} \]
APPEARS IN
संबंधित प्रश्न
For the following differential equation verify that the accompanying function is a solution:
| Differential equation | Function |
|
\[x\frac{dy}{dx} = y\]
|
y = ax |
For the following differential equation verify that the accompanying function is a solution:
| Differential equation | Function |
|
\[x^3 \frac{d^2 y}{d x^2} = 1\]
|
\[y = ax + b + \frac{1}{2x}\]
|
Differential equation \[x\frac{dy}{dx} = 1, y\left( 1 \right) = 0\]
Function y = log x
Solve the following differential equation:
\[y e^\frac{x}{y} dx = \left( x e^\frac{x}{y} + y^2 \right)dy, y \neq 0\]
Solve the following differential equation:
\[\left( 1 + y^2 \right) \tan^{- 1} xdx + 2y\left( 1 + x^2 \right)dy = 0\]
The volume of a spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of the balloon after `t` seconds.
x2 dy + y (x + y) dx = 0
In a culture, the bacteria count is 100000. The number is increased by 10% in 2 hours. In how many hours will the count reach 200000, if the rate of growth of bacteria is proportional to the number present?
A bank pays interest by continuous compounding, that is, by treating the interest rate as the instantaneous rate of change of principal. Suppose in an account interest accrues at 8% per year, compounded continuously. Calculate the percentage increase in such an account over one year.
The slope of the tangent at a point P (x, y) on a curve is \[\frac{- x}{y}\]. If the curve passes through the point (3, −4), find the equation of the curve.
Define a differential equation.
The solution of the differential equation y1 y3 = y22 is
What is integrating factor of \[\frac{dy}{dx}\] + y sec x = tan x?
Solve the following differential equation : \[\left( \sqrt{1 + x^2 + y^2 + x^2 y^2} \right) dx + xy \ dy = 0\].
Determine the order and degree of the following differential equations.
| Solution | D.E |
| y = aex + be−x | `(d^2y)/dx^2= 1` |
For each of the following differential equations find the particular solution.
`y (1 + logx)dx/dy - x log x = 0`,
when x=e, y = e2.
Solve the following differential equation.
xdx + 2y dx = 0
Solve the following differential equation.
(x2 − y2 ) dx + 2xy dy = 0
Solve the following differential equation.
`dy/dx + y` = 3
State whether the following is True or False:
The integrating factor of the differential equation `dy/dx - y = x` is e-x
Solve `("d"y)/("d"x) = (x + y + 1)/(x + y - 1)` when x = `2/3`, y = `1/3`
Solve the differential equation (x2 – yx2)dy + (y2 + xy2)dx = 0
Verify y = log x + c is the solution of differential equation `x ("d"^2y)/("d"x^2) + ("d"y)/("d"x)` = 0
Solve the following differential equation `("d"y)/("d"x)` = cos(x + y)
Solution: `("d"y)/("d"x)` = cos(x + y) ......(1)
Put `square`
∴ `1 + ("d"y)/("d"x) = "dv"/("d"x)`
∴ `("d"y)/("d"x) = "dv"/("d"x) - 1`
∴ (1) becomes `"dv"/("d"x) - 1` = cos v
∴ `"dv"/("d"x)` = 1 + cos v
∴ `square` dv = dx
Integrating, we get
`int 1/(1 + cos "v") "d"v = int "d"x`
∴ `int 1/(2cos^2 ("v"/2)) "dv" = int "d"x`
∴ `1/2 int square "dv" = int "d"x`
∴ `1/2* (tan("v"/2))/(1/2)` = x + c
∴ `square` = x + c
The integrating factor of the differential equation `"dy"/"dx" (x log x) + y` = 2logx is ______.
Solve the differential equation `"dy"/"dx"` = 1 + x + y2 + xy2, when y = 0, x = 0.
The differential equation of all non horizontal lines in a plane is `("d"^2x)/("d"y^2)` = 0
There are n students in a school. If r % among the students are 12 years or younger, which of the following expressions represents the number of students who are older than 12?
A man is moving away from a tower 41.6 m high at a rate of 2 m/s. If the eye level of the man is 1.6 m above the ground, then the rate at which the angle of elevation of the top of the tower changes, when he is at a distance of 30 m from the foot of the tower, is
