Question

\[\frac{dy}{dx} = x \log x\]

Answer 1

We have, 
\[\frac{dy}{dx} = x \log x\]
\[ \Rightarrow dy = \left( x \log x \right)dx\]
Integrating both sides, we get
\[\int dy = \int\left( x \log x \right)dx\]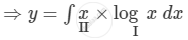

\[ \Rightarrow y = \log x\int x\ dx - \int\left[ \frac{d}{dx}\left( \log x \right)\int x\ dx \right]dx\]
\[ \Rightarrow y = \log x \times \frac{x^2}{2} - \int\left( \frac{1}{x} \times \frac{x^2}{2} \right)dx\]
\[ \Rightarrow y = \frac{1}{2} x^2 \log x - \int\frac{x}{2}dx\]
\[ \Rightarrow y = \frac{1}{2} x^2 \log x - \frac{x^2}{4} + C\]
\[ \text{ Hence, }y = \frac{1}{2} x^2 \log x - \frac{x^2}{4} + \text{C is the solution to the given differential equation.}\]