Advertisements
Advertisements
Question
Solve the following differential equation:-
\[\frac{dy}{dx} + 2y = \sin x\]
Advertisements
Solution
We have,
\[\frac{dy}{dx} + 2y = \sin x\]
\[\text{Comparing with }\frac{dy}{dx} + Py = Q,\text{ we get}\]
\[P = 2 \]
\[Q = \sin x\]
Now,
\[I . F . = e^{2\int dx} = e^{2x} \]
Solution is given by,
\[y \times I . F . = \int\sin x \times I . F . dx + C\]
\[ \Rightarrow y e^{2x} = I + C . . . . . \left( 1 \right)\]
Where,
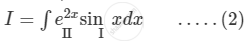
\[ \Rightarrow I = \sin x\int e^{2x} dx - \int\left[ \frac{d}{dx}\left( \sin x \right)\int e^{2x} dx \right]dx\]
\[ \Rightarrow I = \frac{\sin x e^{2x}}{2} - \frac{1}{2}\int\cos x e^{2x} dx\]
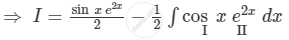
\[ \Rightarrow I = \frac{\sin x e^{2x}}{2} - \frac{1}{2}\cos x\int e^{2x} dx + \frac{1}{2}\int\left[ \frac{d}{dx}\left( \cos x \right)\int e^{2x} dx \right]dx\]
\[ \Rightarrow I = \frac{\sin x e^{2x}}{2} - \frac{1}{4}\cos x e^{2x} - \frac{1}{4}\int\left[ \sin x e^{2x} \right]dx\]
\[ \Rightarrow I = \frac{\sin x e^{2x}}{2} - \frac{1}{4}\cos x e^{2x} - \frac{1}{4}I ............\left[\text{Using (2)} \right]\]
\[ \Rightarrow I + \frac{1}{4}I = \frac{1}{2}\sin x e^{2x} - \frac{1}{4}\cos x e^{2x} \]
\[ \Rightarrow \frac{5}{4}I = \frac{1}{4}\left( 2\sin x e^{2x} - \cos x e^{2x} \right)\]
\[ \Rightarrow I = \frac{1}{5}\left( 2\sin x - \cos x \right) e^{2x} . . . . . \left( 3 \right)\]
Therefore from (1) and (3), we get
\[ \therefore y e^{2x} = \frac{1}{5}\left( 2\sin x - \cos x \right) e^{2x} + C\]
\[ \Rightarrow y = \frac{1}{5}\left( 2 \sin x - \cos x \right) + C e^{- 2x}\]
