Advertisements
Advertisements
प्रश्न
If sin x = cos x and x is acute, state the value of x
उत्तर
The angle, x is acute and hence we have, 0 < x
We know that
cos2x + sin2 x = 1
⇒ 2sin2 x = 1
⇒ sin x = `(1)/(sqrt2)`
⇒ x = 45°
APPEARS IN
संबंधित प्रश्न
Find the value of x in the following :
tan 3x = sin 45º cos 45º + sin 30º
Evaluate the following:
`(5cos^2 60° + 4sec^2 30° - tan^2 45°)/(sin^2 30° + cos^2 30°)`
`(1- tan^2 45°)/(1+tan^2 45°)` = ______
`(2 tan 30°)/(1-tan^2 30°)` = ______.
State whether the following is true or false. Justify your answer.
sinθ = cosθ for all values of θ.
find the value of: sin 30° cos 30°
prove that:
sin (2 × 30°) = `(2 tan 30°)/(1+tan^2 30°)`
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratios: sin 45°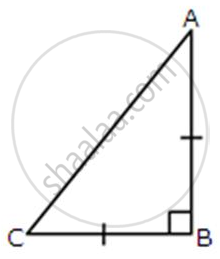
If sin x = cos y, then x + y = 45° ; write true of false
find the value of :
3sin2 30° + 2tan2 60° - 5cos2 45°
Prove that:
cosec2 45° - cot2 45° = 1
Prove that:
cos2 30° - sin2 30° = cos 60°
If sin x = cos y; write the relation between x and y, if both the angles x and y are acute.
If A = 30°;
show that:
`(cos^3"A" – cos 3"A")/(cos "A") + (sin^3"A" + sin3"A")/(sin"A") = 3`
Without using tables, evaluate the following: cosec245° sec230° - sin230° - 4cot245° + sec260°.
Without using tables, evaluate the following: cosec330° cos60° tan345° sin290° sec245° cot30°.
Without using tables, find the value of the following: `(tan45°)/("cosec"30°) + (sec60°)/(cot45°) - (5sin90°)/(2cos0°)`
Prove that : sec245° - tan245° = 1
Find the value of x in the following: `2sin x/(2)` = 1
Find the value of x in the following: `sqrt(3)sin x` = cos x
If sinθ = cosθ and 0° < θ<90°, find the value of 'θ'.
If sin(A +B) = 1(A -B) = 1, find A and B.
Verify the following equalities:
1 + tan2 30° = sec2 30°
Find the value of the following:
sin2 30° – 2 cos3 60° + 3 tan4 45°
The value of `(2tan30^circ)/(1 - tan^2 30^circ)` is equal to
The value of cos1°. cos2°. cos3°. cos4°....................... cos90° is ______.
Evaluate: `(5cos^2 60° + 4sec^2 30° - tan^2 45°)/(sin^2 30° + sin^2 60°)`
