Advertisements
Advertisements
प्रश्न
The domain of definition of the function \[f\left( x \right) = \sqrt{x - 1} + \sqrt{3 - x}\] is
पर्याय
(a) [1, ∞)
(b) (−∞, 3)
(c) (1, 3)
(d) [1, 3]
उत्तर
(d) [1, 3]
\[\text{ For f(x) to be defined, } \]
\[\left( x - 1 \right) \geq 0\]
\[ \Rightarrow x \geq 1 . . . (1)\]
\[\text{ and } \left( 3 - x \right) \geq 0\]
\[ \Rightarrow 3 \leq x . . . (2)\]
\[\text{ From (1) and (2), } \]
\[x \in [1, 3]\]
APPEARS IN
संबंधित प्रश्न
If f(x) = (x − a)2 (x − b)2, find f(a + b).
If f(x) = 4x − x2, x ∈ R, then write the value of f(a + 1) −f(a − 1).
Find the set of values of x for which the functions f(x) = 3x2 − 1 and g(x) = 3 + x are equal.
Let A = {1, 2, 3} and B = {2, 3, 4}. Then which of the following is a function from A to B?
If f(x) = cos (log x), then the value of f(x) f(y) −\[\frac{1}{2}\left\{ f\left( \frac{x}{y} \right) + f\left( xy \right) \right\}\] is
If A = {1, 2, 3} and B = {x, y}, then the number of functions that can be defined from A into B is
If \[f\left( x \right) = \frac{2^x + 2^{- x}}{2}\] , then f(x + y) f(x − y) is equal to
The function f : R → R is defined by f(x) = cos2 x + sin4 x. Then, f(R) =
If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =
Let \[f\left( x \right) = \sqrt{x^2 + 1}\ ] . Then, which of the following is correct?
If f(m) = m2 − 3m + 1, find f(−3)
If f(x) =` (2x−1)/ (5x−2) , x ≠ 2/5` Verify whether (fof) (x) = x
Find x, if f(x) = g(x) where f(x) = `sqrt(x) - 3`, g(x) = 5 – x
Express the area A of circle as a function of its radius r
Express the following exponential equation in logarithmic form
3–4 = `1/81`
Write the following expression as sum or difference of logarithm
`log ("pq"/"rs")`
If x = loga bc, y = logb ca, z = logc ab then prove that `1/(1 + x) + 1/(1 + y) + 1/(1 + z)` = 1
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f − g) (2)
Select the correct answer from given alternatives
If f(x) = 2x2 + bx + c and f(0) = 3 and f(2) = 1, then f(1) is equal to
Select the correct answer from given alternative.
The domain and range of f(x) = 2 − |x − 5| is
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range
{(12, 1), (3, 1), (5, 2)}
Answer the following:
Find whether the following function is one-one
f : R → R defined by f(x) = x2 + 5
Answer the following:
Let f : R → R be given by f(x) = x3 + 1 for all x ∈ R. Draw its graph
Answer the following:
Show that, `log |sqrt(x^2 + 1) + x | + log | sqrt(x^2 + 1) - x|` = 0
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
If a2 + b2 = 7ab, show that, `log(("a" + "b")/3) = 1/2 log "a" + 1/2 log "b"`
Answer the following:
If `log ((x - y)/5) = 1/2 logx + 1/2 log y`, show that x2 + y2 = 27xy
Answer the following:
Without using log tables, prove that `2/5 < log_10 3 < 1/2`
Answer the following:
Find the range of the following function.
f(x) = |x – 5|
Given the function f: x → x2 – 5x + 6, evaluate f(2)
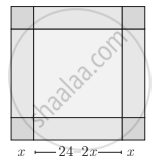
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal square from the corner and turning up the side as shown. Express the volume V of the box as a function of x
If f(x) = `1/sqrt(4 - 3x)`, then dom(f) = ______..
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
Find the range of the following functions given by f(x) = 1 – |x – 2|
The value of the function f(x) = `(x^2 - 3x + 2)/(x^2 + x - 6)` lies in the interval
The domain of the function f(x) = `sin^-1((|x| + 5)/(x^2 + 1))` is (–∞, –a] ≈ [a, ∞). Then a is equal to ______.
If f : R – {2} `rightarrow` R i s a function defined by f(x) = `(x^2 - 4)/(x - 2)`, then its range is ______.
