Question

Find the equation of the curve which passes through the origin and has the slope x + 3y− 1 at any point (x, y) on it.

Answer 1

According to the question,
\[\frac{dy}{dx} = x + 3y - 1\]
\[\Rightarrow \frac{dy}{dx} - 3y = x - 1\]
\[\text{ Comparing with }\frac{dy}{dx} + Py = Q,\text{ we get }\]
\[P = - 3 \]
\[Q = x - 1\]
Now, 
\[I . F . = e^{- \int3dx} = e^{- 3x} \]
So, the solution is given by
\[y \times I . F . = \int Q \times I . F . dx + C\]
\[ \Rightarrow y e^{- 3x} = \int\left( x - 1 \right) e^{- 3x} dx + C\]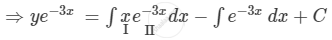

\[ \Rightarrow y e^{- 3x} = x\int e^{- 3x} dx - \int\left[ \frac{d}{dx}\left( x \right)\int e^{- 3x} dx \right]dx - \int e^{- 3x} dx + C\]
\[ \Rightarrow y e^{- 3x} = - \frac{1}{3}x e^{- 3x} + \frac{1}{3}\int e^{- 3x} dx - \int e^{- 3x} dx + C\]
\[ \Rightarrow y e^{- 3x} = - \frac{1}{3}x e^{- 3x} - \frac{1}{9} e^{- 3x} + \frac{1}{3} e^{- 3x} + C\]
\[ \Rightarrow y = - \frac{1}{3}x - \frac{1}{9} + \frac{1}{3} + C e^{3x} \]
\[ \Rightarrow y = - \frac{1}{3}x + \frac{2}{9} + C e^{3x} \]
Since the curve passes throught the origin, it satisfies the equation of the curve. 
\[ \Rightarrow 0 = - 0 + \frac{2}{9} + C e^0 \]
\[ \Rightarrow C = - \frac{2}{9}\]
Putting the value of C in the equation of the curve, we get
\[y = - \frac{1}{3}x + \frac{2}{9}\left( 1 - e^{3x} \right)\]
\[ \Rightarrow y + \frac{1}{3}x = \frac{2}{9}\left( 1 - e^{3x} \right)\]
\[ \Rightarrow 3\left( 3y + x \right) = 2\left( 1 - e^{3x} \right)\]