Advertisements
Advertisements
प्रश्न
Find the equation of the curve which passes through the origin and has the slope x + 3y− 1 at any point (x, y) on it.
उत्तर
According to the question,
\[\frac{dy}{dx} = x + 3y - 1\]
\[\Rightarrow \frac{dy}{dx} - 3y = x - 1\]
\[\text{ Comparing with }\frac{dy}{dx} + Py = Q,\text{ we get }\]
\[P = - 3 \]
\[Q = x - 1\]
Now,
\[I . F . = e^{- \int3dx} = e^{- 3x} \]
So, the solution is given by
\[y \times I . F . = \int Q \times I . F . dx + C\]
\[ \Rightarrow y e^{- 3x} = \int\left( x - 1 \right) e^{- 3x} dx + C\]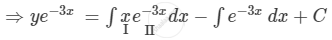
\[ \Rightarrow y e^{- 3x} = x\int e^{- 3x} dx - \int\left[ \frac{d}{dx}\left( x \right)\int e^{- 3x} dx \right]dx - \int e^{- 3x} dx + C\]
\[ \Rightarrow y e^{- 3x} = - \frac{1}{3}x e^{- 3x} + \frac{1}{3}\int e^{- 3x} dx - \int e^{- 3x} dx + C\]
\[ \Rightarrow y e^{- 3x} = - \frac{1}{3}x e^{- 3x} - \frac{1}{9} e^{- 3x} + \frac{1}{3} e^{- 3x} + C\]
\[ \Rightarrow y = - \frac{1}{3}x - \frac{1}{9} + \frac{1}{3} + C e^{3x} \]
\[ \Rightarrow y = - \frac{1}{3}x + \frac{2}{9} + C e^{3x} \]
Since the curve passes throught the origin, it satisfies the equation of the curve.
\[ \Rightarrow 0 = - 0 + \frac{2}{9} + C e^0 \]
\[ \Rightarrow C = - \frac{2}{9}\]
Putting the value of C in the equation of the curve, we get
\[y = - \frac{1}{3}x + \frac{2}{9}\left( 1 - e^{3x} \right)\]
\[ \Rightarrow y + \frac{1}{3}x = \frac{2}{9}\left( 1 - e^{3x} \right)\]
\[ \Rightarrow 3\left( 3y + x \right) = 2\left( 1 - e^{3x} \right)\]
APPEARS IN
संबंधित प्रश्न
Differential equation \[\frac{d^2 y}{d x^2} - 2\frac{dy}{dx} + y = 0, y \left( 0 \right) = 1, y' \left( 0 \right) = 2\] Function y = xex + ex
(y + xy) dx + (x − xy2) dy = 0
Find the particular solution of the differential equation \[\frac{dy}{dx} = - 4x y^2\] given that y = 1, when x = 0.
In a culture the bacteria count is 100000. The number is increased by 10% in 2 hours. In how many hours will the count reach 200000, if the rate of growth of bacteria is proportional to the number present.
Solve the following initial value problem:-
\[\left( 1 + y^2 \right) dx + \left( x - e^{- \tan^{- 1} y} \right) dx = 0, y\left( 0 \right) = 0\]
Solve the following initial value problem:
\[x\frac{dy}{dx} + y = x \cos x + \sin x, y\left( \frac{\pi}{2} \right) = 1\]
The rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given the number triples in 5 hrs, find how many bacteria will be present after 10 hours. Also find the time necessary for the number of bacteria to be 10 times the number of initial present.
The integrating factor of the differential equation (x log x)
\[\frac{dy}{dx} + y = 2 \log x\], is given by
The differential equation \[x\frac{dy}{dx} - y = x^2\], has the general solution
The differential equation
\[\frac{dy}{dx} + Py = Q y^n , n > 2\] can be reduced to linear form by substituting
Integrating factor of the differential equation cos \[x\frac{dy}{dx} + y \sin x = 1\], is
The integrating factor of the differential equation \[x\frac{dy}{dx} - y = 2 x^2\]
For the following differential equation find the particular solution.
`(x + 1) dy/dx − 1 = 2e^(−y)`,
when y = 0, x = 1
Solve the following differential equation.
y2 dx + (xy + x2 ) dy = 0
Solve the following differential equation.
`xy dy/dx = x^2 + 2y^2`
Solve the following differential equation.
y dx + (x - y2 ) dy = 0
Solve the following differential equation.
dr + (2r)dθ= 8dθ
Choose the correct alternative.
The differential equation of y = `k_1 + k_2/x` is
`xy dy/dx = x^2 + 2y^2`
Select and write the correct alternative from the given option for the question
Bacterial increases at the rate proportional to the number present. If original number M doubles in 3 hours, then number of bacteria will be 4M in
Solve the differential equation sec2y tan x dy + sec2x tan y dx = 0
Solve the following differential equation
`x^2 ("d"y)/("d"x)` = x2 + xy − y2
State whether the following statement is True or False:
The integrating factor of the differential equation `("d"y)/("d"x) - y` = x is e–x
Solve: ydx – xdy = x2ydx.
The differential equation of all non horizontal lines in a plane is `("d"^2x)/("d"y^2)` = 0
`d/(dx)(tan^-1 (sqrt(1 + x^2) - 1)/x)` is equal to:
Solve the differential equation
`y (dy)/(dx) + x` = 0
