Advertisements
Advertisements
Question
There are two poles, one each on either bank of a river just opposite to each other. One pole is 60 m high. From the top of this pole, the angle of depression of the top and foot of the other pole are 30° and 60° respectively. Find the width of the river and height of the other pole.
Solution
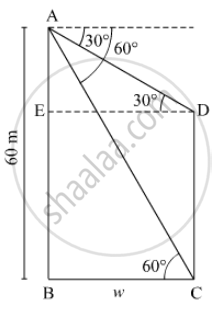
Let the width of the river be w.
In ΔABC,
tan 60° = `"AB"/"BC"`
⇒ `sqrt3` = `60/w`
⇒ w = `60/(sqrt3) = (60sqrt3)/3= 20sqrt3`
In △AED,
tan30° = `"AE"/"ED"`
⇒ `1/(sqrt3) = "AE"/w`
⇒ `1/(sqrt3) = "AE"/(20sqrt3)`
⇒ AE = 20
Height of pole CD = AB − AE
= 60 − 20 = 40 m.
Thus, width of river is `20sqrt3` = 20 x 1.732 = 34.64 m
Height of pole = 40 m.
RELATED QUESTIONS
`"If "\frac{\cos \alpha }{\cos \beta }=m\text{ and }\frac{\cos \alpha }{\sin \beta }=n " show that " (m^2 + n^2 ) cos^2 β = n^2`
Prove the following trigonometric identities.
`cot^2 A cosec^2B - cot^2 B cosec^2 A = cot^2 A - cot^2 B`
Prove the following trigonometric identities
If x = a sec θ + b tan θ and y = a tan θ + b sec θ, prove that x2 − y2 = a2 − b2
Prove the following trigonometric identities.
if cos A + cos2 A = 1, prove that sin2 A + sin4 A = 1
Prove the following identities:
cosec4 A – cosec2 A = cot4 A + cot2 A
Prove the following identities:
`1/(sinA + cosA) + 1/(sinA - cosA) = (2sinA)/(1 - 2cos^2A)`
Prove that:
2 sin2 A + cos4 A = 1 + sin4 A
Prove the following identities:
`cotA/(1 - tanA) + tanA/(1 - cotA) = 1 + tanA + cotA`
`(1-cos^2theta) sec^2 theta = tan^2 theta`
`1+((tan^2 theta) cot theta)/(cosec^2 theta) = tan theta`
If `sin theta = x , " write the value of cot "theta .`
\[\frac{1 - \sin \theta}{\cos \theta}\] is equal to
If x = a cos θ and y = b sin θ, then b2x2 + a2y2 =
Prove the following identity :
`2(sin^6θ + cos^6θ) - 3(sin^4θ + cos^4θ) + 1 = 0`
If tan θ = 2, where θ is an acute angle, find the value of cos θ.
Prove that cot θ. tan (90° - θ) - sec (90° - θ). cosec θ + 1 = 0.
Proved that cosec2(90° - θ) - tan2 θ = cos2(90° - θ) + cos2 θ.
Prove that `(tan θ + sin θ)/(tan θ - sin θ) = (sec θ + 1)/(sec θ - 1)`
Choose the correct alternative:
Which is not correct formula?
Prove that `1/("cosec" theta - cot theta)` = cosec θ + cot θ
