Advertisements
Advertisements
प्रश्न
There are two poles, one each on either bank of a river just opposite to each other. One pole is 60 m high. From the top of this pole, the angle of depression of the top and foot of the other pole are 30° and 60° respectively. Find the width of the river and height of the other pole.
उत्तर
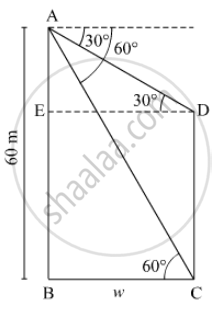
Let the width of the river be w.
In ΔABC,
tan 60° = `"AB"/"BC"`
⇒ `sqrt3` = `60/w`
⇒ w = `60/(sqrt3) = (60sqrt3)/3= 20sqrt3`
In △AED,
tan30° = `"AE"/"ED"`
⇒ `1/(sqrt3) = "AE"/w`
⇒ `1/(sqrt3) = "AE"/(20sqrt3)`
⇒ AE = 20
Height of pole CD = AB − AE
= 60 − 20 = 40 m.
Thus, width of river is `20sqrt3` = 20 x 1.732 = 34.64 m
Height of pole = 40 m.
संबंधित प्रश्न
Prove that:
sec2θ + cosec2θ = sec2θ x cosec2θ
If (secA + tanA)(secB + tanB)(secC + tanC) = (secA – tanA)(secB – tanB)(secC – tanC) prove that each of the side is equal to ±1. We have,
`"If "\frac{\cos \alpha }{\cos \beta }=m\text{ and }\frac{\cos \alpha }{\sin \beta }=n " show that " (m^2 + n^2 ) cos^2 β = n^2`
Prove the following trigonometric identities.
`(1 - cos theta)/sin theta = sin theta/(1 + cos theta)`
Prove the following trigonometric identities.
`(1 - sin theta)/(1 + sin theta) = (sec theta - tan theta)^2`
Prove the following trigonometric identities.
sin2 A cot2 A + cos2 A tan2 A = 1
Prove the following trigonometric identities.
`cot^2 A cosec^2B - cot^2 B cosec^2 A = cot^2 A - cot^2 B`
Prove the following identities:
(cosec A – sin A) (sec A – cos A) (tan A + cot A) = 1
Prove the following identities:
(sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2 A + cot2 A
Prove the following identities:
`1 - sin^2A/(1 + cosA) = cosA`
If sin A + cos A = p and sec A + cosec A = q, then prove that : q(p2 – 1) = 2p.
If `sec theta + tan theta = x," find the value of " sec theta`
Prove that:
`"tanθ"/("secθ" – 1) = (tanθ + secθ + 1)/(tanθ + secθ - 1)`
sec4 A − sec2 A is equal to
Prove the following identity :
`(sinA - sinB)/(cosA + cosB) + (cosA - cosB)/(sinA + sinB) = 0`
Prove that `((1 + sin θ - cos θ)/( 1 + sin θ + cos θ))^2 = (1 - cos θ)/(1 + cos θ)`.
Prove that cos θ sin (90° - θ) + sin θ cos (90° - θ) = 1.
Prove the following identities: cot θ - tan θ = `(2 cos^2 θ - 1)/(sin θ cos θ)`.
Show that tan 7° × tan 23° × tan 60° × tan 67° × tan 83° = `sqrt(3)`
Complete the following activity to prove:
cotθ + tanθ = cosecθ × secθ
Activity: L.H.S. = cotθ + tanθ
= `cosθ/sinθ + square/cosθ`
= `(square + sin^2theta)/(sinθ xx cosθ)`
= `1/(sinθ xx cosθ)` ....... ∵ `square`
= `1/sinθ xx 1/cosθ`
= `square xx secθ`
∴ L.H.S. = R.H.S.
