Advertisements
Advertisements
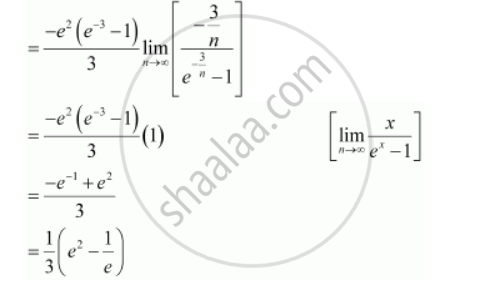
प्रश्न
Evaluate `int_0^1 e^(2-3x) dx` as a limit of a sum.
उत्तर


APPEARS IN
संबंधित प्रश्न
Evaluate `int_(-1)^2(e^3x+7x-5)dx` as a limit of sums
Evaluate the following definite integrals as limit of sums.
`int_0^5 (x+1) dx`
Evaluate the following definite integrals as limit of sums.
`int_0^4 (x + e^(2x)) dx`
Evaluate the definite integral:
`int_0^(pi/4) (sinx cos x)/(cos^4 x + sin^4 x)`dx
Evaluate the definite integral:
`int_0^1 dx/(sqrt(1+x) - sqrtx)`
Evaluate the definite integral:
`int_0^(pi/2) sin 2x tan^(-1) (sinx) dx`
Evaluate the definite integral:
`int_1^4 [|x - 1|+ |x - 2| + |x -3|]dx`
Prove the following:
`int_0^(pi/4) 2 tan^3 xdx = 1 - log 2`
Prove the following:
`int_0^1sin^(-1) xdx = pi/2 - 1`
\[\int\frac{1}{x} \left( \log x \right)^2 dx\]
Evaluate the following integrals as limit of sums:
\[\int\frac{\sqrt{\tan x}}{\sin x \cos x} dx\]
Using L’Hospital Rule, evaluate: `lim_(x->0) (8^x - 4^x)/(4x
)`
Evaluate `int_1^4 ( 1+ x +e^(2x)) dx` as limit of sums.
Evaluate:
`int (sin"x"+cos"x")/(sqrt(9+16sin2"x")) "dx"`
If f and g are continuous functions in [0, 1] satisfying f(x) = f(a – x) and g(x) + g(a – x) = a, then `int_0^"a" "f"(x) * "g"(x)"d"x` is equal to ______.
Evaluate the following as limit of sum:
`int _0^2 (x^2 + 3) "d"x`
Evaluate the following as limit of sum:
`int_0^2 "e"^x "d"x`
Evaluate the following:
`int_0^(pi/2) (tan x)/(1 + "m"^2 tan^2x) "d"x`
Evaluate the following:
`int_0^1 (x"d"x)/sqrt(1 + x^2)`
Evaluate the following:
`int_0^pi x sin x cos^2x "d"x`
The value of `lim_(x -> 0) [(d/(dx) int_0^(x^2) sec^2 xdx),(d/(dx) (x sin x))]` is equal to
If f" = C, C ≠ 0, where C is a constant, then the value of `lim_(x -> 0) (f(x) - 2f (2x) + 3f (3x))/x^2` is
The limit of the function defined by `f(x) = {{:(|x|/x",", if x ≠ 0),(0",", "otherwisw"):}`
